https://www.acmicpc.net/problem/2583
2583번: 영역 구하기
첫째 줄에 M과 N, 그리고 K가 빈칸을 사이에 두고 차례로 주어진다. M, N, K는 모두 100 이하의 자연수이다. 둘째 줄부터 K개의 줄에는 한 줄에 하나씩 직사각형의 왼쪽 아래 꼭짓점의 x, y좌표값과 오
www.acmicpc.net
- 문제
- 풀이 방법
이 문제는 전형적인 영역의 개수를 구하는 그래프 문제이다. 이런 문제 유형이 많으므로 조금만 풀면 이 유형의 그래프 문제는 쉽게 풀 수 있을 것이다. 조금 더 많은 그래프의 정보를 원한다면 밑에 있는 링크를 참고하면 되겠다.
https://propercoding.tistory.com/entry/자료구조-그래프 Graph
[자료구조] 그래프(Graph)
목차 그래프란? 그래프는 정점과 간선으로 이루어진 자료구조임. → 트리는 그래프의 일종인데 다만 트리와는 달리 그래프는 정점마다 간선이 없을 수도 있고 있을 수도 있으며, 루트 노드,
propercoding.tistory.com
이 문제는 주어지는 직사각형의 내부를 제외한 나머지 부분이 몇 개의 분리된 영역으로 나누어지는지, 그리고 분리된 각 영역의 넓이가 몇인지를 구하는 간단한 문제이다. 이 문제는 BFS (너비 우선 탐색) 또는 DFS (깊이 우선 탐색)을 써서 풀 수 있는 문제이다. 일단 주어지는 직사각형을 그래프에 표시를 한 다음에 BFS나 DFS를 써서 표시 안 된 영역의 개수와 표시 안 된 영역의 넓이를 오름차순으로 출력해주면 된다.
오름차순으로 값을 출력하는 거는 List를 이용해서 해결을 했다. 영역의 넓이를 구할 때마다 list에 삽입을 하고 마지막에 List를 정렬한 후 한꺼번에 StringBuilder에 넣어 출력하는 방식으로 했다.
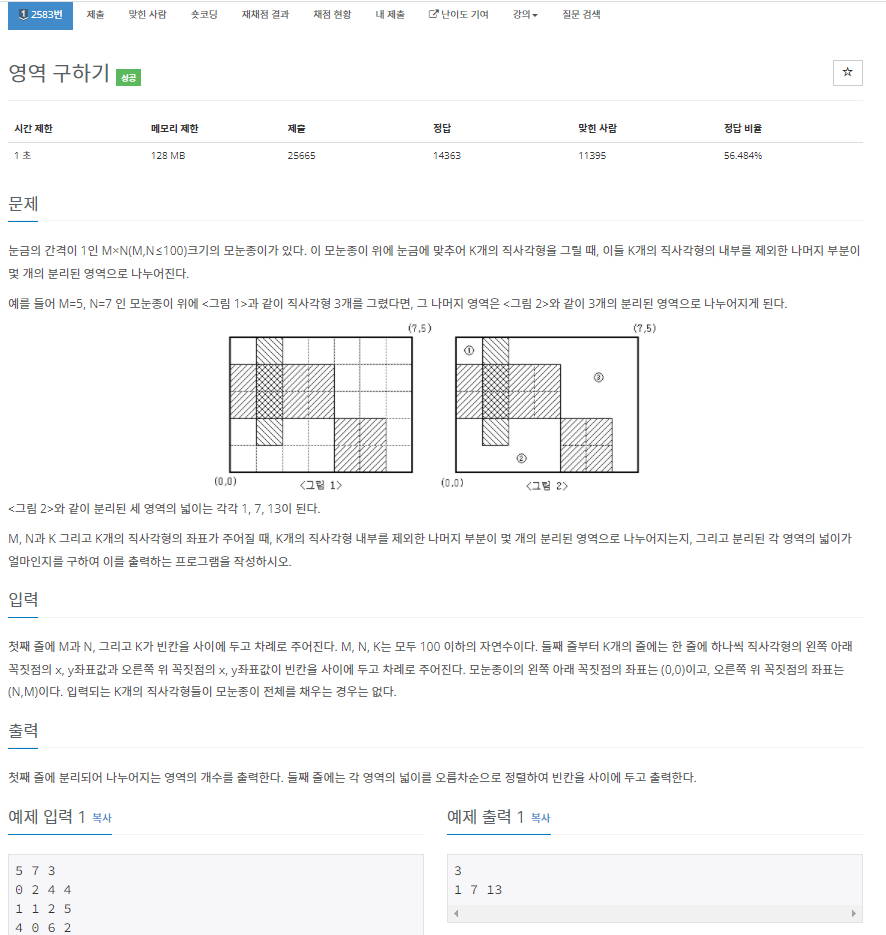
예제를 보면 다음과 같이 3개의 영역이 나온다. 그리고 A의 넓이는 1, B의 넓이는 13, C의 넓이는 7이다.
이것을 List에 넣으면 {1, 13, 7}이고 정렬을 하면 {1, 7, 13} 이 된다. 따라서 원하는 답을 출력할 수 있다.

- 풀이
import java.io.*;
import java.util.*;
public class Main {
static boolean[][] graph;
static List<Integer> list;
static int count;
static int m;
static int n;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
m = Integer.parseInt(st.nextToken());
n = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
list = new ArrayList<>();
count = 0;
graph = new boolean[m][n];
for (int i = 0; i < k; i++) {
st = new StringTokenizer(br.readLine());
int n1 = Integer.parseInt(st.nextToken());
int m1 = Integer.parseInt(st.nextToken());
int n2 = Integer.parseInt(st.nextToken())-1;
int m2 = Integer.parseInt(st.nextToken())-1;
for (int j = m1; j <= m2; j++) {
for (int l = n1; l <= n2; l++) {
graph[j][l] = true;
}
}
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (!graph[i][j]) {
count = 1;
graph[i][j] = true;
dfs(i,j);
list.add(count);
}
}
}
StringBuilder sb = new StringBuilder();
Collections.sort(list);
sb.append(list.size() + "\n");
for (int i = 0; i < list.size(); i++) {
sb.append(list.get(i) + " ");
}
System.out.print(sb);
}
static void dfs(int y, int x) {
if (y > 0 && !graph[y-1][x]) {
graph[y-1][x] = true;
dfs(y-1,x);
count++;
}
if (y < m-1 && !graph[y+1][x]) {
graph[y+1][x] = true;
dfs(y+1,x);
count++;
}
if (x > 0 && !graph[y][x-1]) {
graph[y][x-1] = true;
dfs(y,x-1);
count++;
}
if (x < n-1 && !graph[y][x+1]) {
graph[y][x+1] = true;
dfs(y, x+1);
count++;
}
}
}
- 후기
이 문제는 전형적인 영역을 구하는 그래프 문제였던 거 같다. BFS나 DFS, 그리고 기본 그래프의 원리를 알면 쉽게 풀 수 있는 문제인 거 같다. 앞으로는 실버 문제만 풀지 말고 조금 더 어렵고 시간이 오래 걸려도 골드 문제를 도전해봐야 될 거 같다.
'백준' 카테고리의 다른 글
| [백준] 9465번 : 스티커 – JAVA [자바] (0) | 2022.02.11 |
|---|---|
| [백준] 2293번 : 동전 1 – JAVA [자바] (0) | 2022.02.05 |
| [백준] 10026번 : 적록색약 – JAVA [자바] (1) | 2022.01.31 |
| [백준] 15482번 : 한글 LCS – JAVA [자바] (0) | 2022.01.30 |
| [백준] 16948번 : 데스 나이트 – JAVA [자바] (0) | 2022.01.29 |




댓글