https://www.acmicpc.net/problem/9084
9084번: 동전
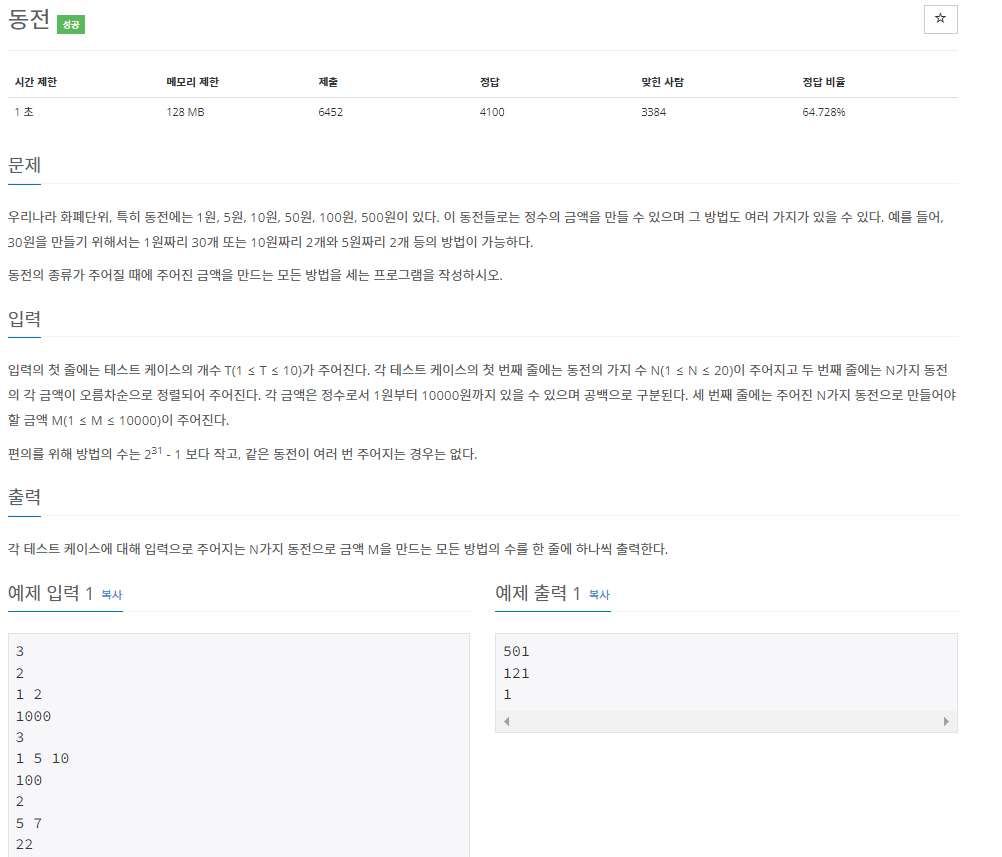
우리나라 화폐단위, 특히 동전에는 1원, 5원, 10원, 50원, 100원, 500원이 있다. 이 동전들로는 정수의 금액을 만들 수 있으며 그 방법도 여러 가지가 있을 수 있다. 예를 들어, 30원을 만들기 위해서는
www.acmicpc.net
- 문제
- 문제 풀이
백준 9084번은 골드 5 난이도의 DP (다이나믹 프로그래밍) 문제다. 특히 이 문제는 전에 올렸던 백준 2293번 동전 1과 거의 똑같으니 밑에 링크를 참고해도 좋겠다.
https://propercoding.tistory.com/entry/백준-2293번-영역-구하기-–-JAVA-자바
[백준] 2293번 : 동전 1 – JAVA [자바]
https://www.acmicpc.net/problem/2293 2293번: 동전 1 첫째 줄에 n, k가 주어진다. (1 ≤ n ≤ 100, 1 ≤ k ≤ 10,000) 다음 n개의 줄에는 각각의 동전의 가치가 주어진다. 동전의 가치는 100,000보다 작거나 같..
propercoding.tistory.com
이 문제에는 T개의 테스트 케이스, 동전의 가지 수 N, 그리고 이 N가지 동전으로 만들어야 할 금액 M이 주어진다. 따라서 N가지의 동전으로 M원을 만드는 방법의 수를 T번 구하면 되는 문제이다.
이 문제에서는 1차원 배열 dp를 만들어서 풀면 된다.
dp [i] = j, 여기서 i = 금액, j = i원을 만들 수 있는 경우의 수로 정의하겠다.
이 문제의 점화식은 다음과 같다.
→ dp [i] = dp [i] + dp [i - coin] 단, i - coin == 0이면 dp [i] = dp [i] + 1
예시를 한번 보겠다.
동전의 개수 n = 3이고 k = 10원이다. 따라서 1원, 2원, 그리고 5원짜리 동전으로 10원을 만들 수 있는 경우의 수를 구해야 한다.
1. 1원짜리 동전으로 1원부터 10원까지 만들 수 있는 경우의 수를 구한다.
2. 2원짜리 동전으로 10원까지 만들 수 있는 경우의 수를 구한다. 단, 여기서 1원으로 구한 값을 이용해야 한다. 만약에 1원으로 구한 값을 이용을 안 하면 계산해야 되는 개수가 너무 많아지고 이것은 DP가 아니다.
3. 5원짜리 동전으로 10원까지 만들 수 있는 경우의 수를 구한다. (2원으로 구한 값을 재이용한다.)
1원짜리 동전 이용 시 dp 값
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10(원) |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
2원짜리 동전 이용 시 dp 값
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10(원) |
| 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 | 5 | 6 |
5원짜리 동전 이용 시 dp 값
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10(원) |
| 1 | 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 10 |
따라서 이 예시의 답은 10이 된다.
- 코드
import java.util.*;
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int t = Integer.parseInt(br.readLine());
StringBuilder sb = new StringBuilder();
for (int q = 0; q < t; q++) {
int n = Integer.parseInt(br.readLine());
StringTokenizer st = new StringTokenizer(br.readLine());
int[] coins = new int[n+1];
for (int i = 1; i <= n; i++) {
coins[i] = Integer.parseInt(st.nextToken());
}
int m = Integer.parseInt(br.readLine());
int[] dp = new int[m+1];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <=m; j++) {
if (j - coins[i] > 0) {
dp[j] = dp[j] + dp[j-coins[i]];
} else if (j - coins[i] == 0) {
dp[j]++;
}
}
}
sb.append(dp[m] + "\n");
}
System.out.print(sb);
}
}
- 후기
전에 풀었던 문제랑 크게 다른 거는 없어서 비교적 쉽게 풀 수 있었다.
'백준' 카테고리의 다른 글
| [백준] 9655번 : 돌 게임 – JAVA [자바] (1) | 2022.03.21 |
|---|---|
| [백준] 3986번 : 좋은 단어 – JAVA [자바] (2) | 2022.03.17 |
| [백준] 1697번 : 숨바꼭질 – JAVA [자바] (0) | 2022.02.11 |
| [백준] 9465번 : 스티커 – JAVA [자바] (0) | 2022.02.11 |
| [백준] 2293번 : 동전 1 – JAVA [자바] (0) | 2022.02.05 |




댓글