목차
에라토스테네스의 체란?
에라토스테네스의 체는 소수 판별 알고리즘이다. 소수란 ‘양의 약수를 두 개만 가지는 자연수’를 뜻한다. 즉, 1과 자기 자신만 약수로 가진다. 소수의 예시로는 2, 3, 5, 7, 11, 13 등이 있다. 에라토스테네스의 체는 이런 소수들을 대량으로 빠르고 정확하게 구하는 방법이다.
우선 먼저 가장 기본적인 소수 판별 알고리즘들을 살펴보겠다.
시간 복잡도 O(N)
boolean isPrime(int n) {
for (int i = 2; i < n; i++) {
if (n % i == 0) return false;
}
return true;
}
자연수 n이 소수인지 아닌지 판별하는 가장 쉬운 방법은 2부터 n - 1까지의 수로 나누어 떨어지는지 아닌지 확인하는 것이다. 이때, 나누어 떨어진다면 1과 자기 자신 외에 약수가 있다는 것이므로 소수가 아니게 된다.
이 알고리즘의 시간 복잡도는 O(N)이다. 모든 경우의 수를 확인하면서 약수인지 아닌지를 판별하다 보니 이 알고리즘은 비효율적이라고 볼 수 있다.
시간 복잡도 O(√N)
소수가 아닌 수들은 약수의 대칭을 이룬다. 예를 들어서 10의 경우 2 × 5 = 5 × 2인 것처럼 대칭을 이룬다. 따라서 한 자연수 N의 제곱근까지만 약수의 여부를 확인하면 된다.
boolean isPrime(int n) {
int end = (int)Math.sqrt(n);
for (int i = 2; i <= end; i++) {
if (n % i == 0) return false;
}
return true;
}
이 알고리즘의 시간 복잡도는 O(√N)으로 이전 알고리즘보다 더 효율적이다.
하지만, 이런 알고리즘들은 하나의 자연수가 소수인지 아닌지를 판별하는 알고리즘이다. 대량의 소수를 한 번에 판별할 때 사용하는 알고리즘이 바로 에라토스테네스의 체다.
에라토스테네스의 체 원리
에라토스테네스의 체는 가장 먼저 소수를 판별할 범위만큼 배열을 할당한다. 그리고 그 배열 인덱스에 해당하는 값을 넣어준다.
1부터 100까지 판별하는 예시를 한번 살펴보겠다.
1. 우선 배열을 초기화한다
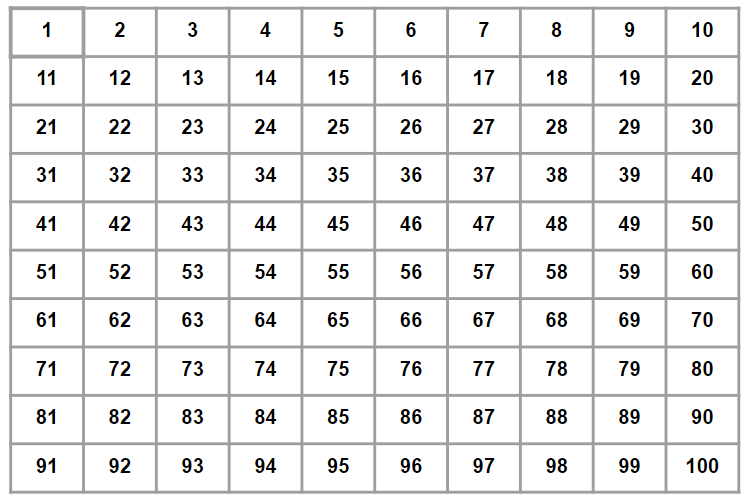
2. 2부터 시작해서 특정 숫자의 배수에 해당하는 숫자들을 모두 지운다
우선 2의 배수들을 지운다. 이때 2 자기 자신은 지우지 않는다. 지운 숫자들을 빨간색으로 표시하겠다.
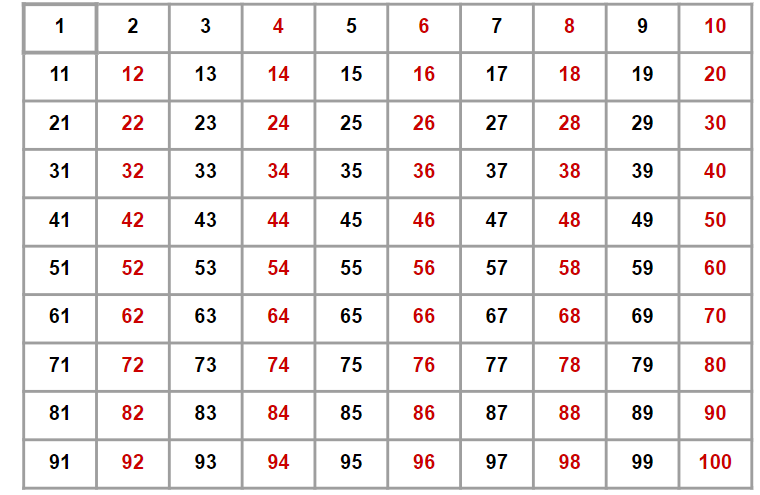
3의 배수도 마찬가지로 지워준다.

3. 이미 지워진 숫자의 경우 건너뛴다
4는 이미 지워졌으므로 지우지 않고 건너뛴다. 이 과정을 N까지 반복한다.
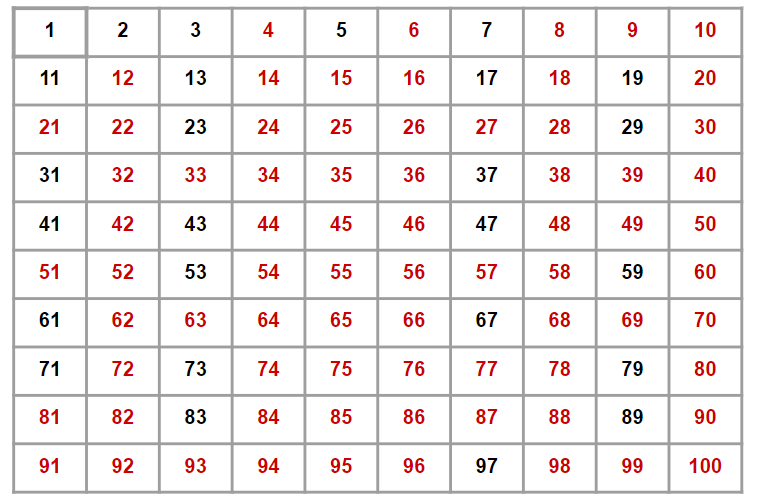
4. 2부터 시작해서 남아있는 숫자들을 출력한다.
남아있는 숫자란 이 배열에서 검은색으로 표시되어 있는 숫자들을 뜻한다. 따라서, 출력을 하면 다음과 같다.
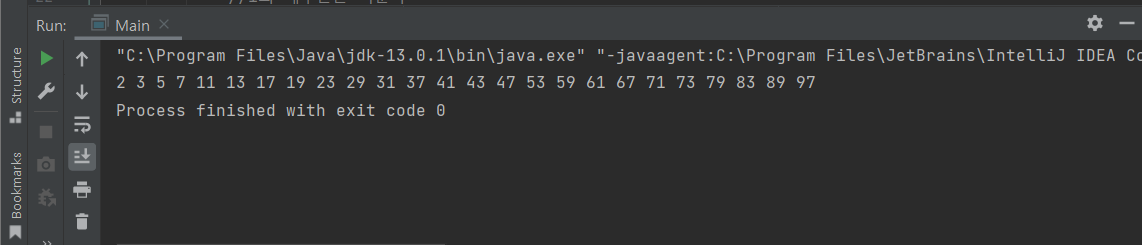
출력 : 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97
소스 코드
public class Main {
static int number; //구하고자 하는 숫자 범위
static int[] arr;
public static void main(String[] args) {
number = 100;
arr = new int[number + 1];
primeNumber();
}
static void primeNumber() {
//배열 초기화
for (int i = 2; i <= number; i++) {
arr[i] = i;
}
for (int i = 2; i <= number; i++) {
//이미 지워진 수는 건너뛴다
if (arr[i] == 0) continue;
//i의 배수들을 지운다
for (int j = i + i; j <= number; j += i) {
arr[j] = 0;
}
}
//소수인 값들은 출력하기
for (int i = 2; i <= number; i++) {
if (arr[i] != 0) System.out.print(i + " ");
}
}
}
이 코드를 실행했을 때 다음과 같은 소수들을 얻는다.
시간 복잡도
에라토스테네스의 체 알고리즘의 시간 복잡도는 O(NloglogN)으로 사실상 O(N) 정도로 빠르다. 그래서 다수의 소수를 찾아야 하는 문제에서 자주 사용된다.
하지만 이 알고리즘은 배열을 N의 크기만큼 할당해야 하기 때문에 메모리가 많이 필요하다는 단점이 있다. 따라서 공간 복잡도면에서는 효율적이지는 않다.
'알고리즘' 카테고리의 다른 글
| [알고리즘] 삽입 정렬 (Insertion Sort) (0) | 2022.07.21 |
|---|---|
| [알고리즘] 버블 정렬 (Bubble Sort) (0) | 2022.07.16 |
| [알고리즘] 선택 정렬 (Selection Sort) (0) | 2022.05.26 |
| [알고리즘] 다익스트라 (Dijkstra) (0) | 2022.05.25 |
| [알고리즘] DFS & BFS (0) | 2022.05.23 |




댓글