목차
이분 탐색이란?
이분 탐색 혹은 이진 탐색 (Binary Search)는 검색 범위를 줄여 나가면서 원하는 데이터를 검색하는 알고리즘이다. 이 알고리즘은 자료가 순서에 따라 정렬된 리스트를 같은 크기의 두 부분 리스트로 나누고 필요한 부분에서만 탐색하도록 제한하여 원하는 원소를 찾는 알고리즘이다. 리스트의 중간 부분에 찾는 원소가 있는지 확인하고, 없으면 위쪽에 있는지 아래쪽에 있는지 판단하여 맨 앞부터 검색하거나 중간부터 검색한다. 따라서, 탐색할 때마다 검사 범위가 절반으로 줄어든다.
이분 탐색 의 진행 단계
이분 탐색에서는 내가 찾고자 하는 값이 정렬된 배열의 중간 값보다 크면 중간값을 포함한 하위 값들은 탐색 대상에서 제외하고, 반대로 찾고자 하는 값이 배열의 중간 값보다 작으면 중간 값을 포함한 상위 값들은 탐색에서 제외해서 탐색을 이어간다.
이분 탐색의 예시를 보겠다. 1부터 100까지 오름차순으로 정렬되어 있는 리스트가 있다. 그리고, 이 리스트에서 77을 찾아보겠다.
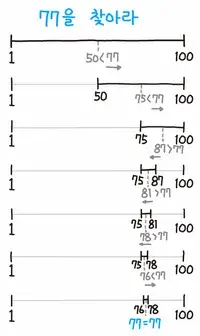
우선 중간값인 50과 77을 비교한다. 77이 50보다 크므로 포인트를 오른쪽으로 이동해서 탐색을 이어간다. 여기서 참고해야 할 점은 중간값인 50이 이미 더 작은 걸 알기 때문에 50 왼쪽에 있는 숫자들 중에서는 77이 있을 수가 없기 때문에 탐색 대상에서 제외한다.
그다음 중간값은 75다. 77과 비교했을 때 77이 더 크므로 50부터 75는 탐색 대상에서 제외하고 75부터 100까지가 탐색 대상이 된다.
그다음 중간값은 87이다. 77과 비교했을 때 77이 더 작으므로 87부터 100은 탐색 대상에서 제외시킨다.
이렇게 이어나가다 보면 범위는 1개가 되고 이 숫자가 찾는 숫자랑 비교했을 때 맞으면 이 숫자를 반환하고 맞지 않으면 false를 반환한다.
이분 탐색 소스 코드
재귀 함수로 구현한 이분 탐색
public class BinarySearch {
// 재귀적 이진 검색 함수
public static int binarySearchRecursive(int[] arr, int number) {
return binarySearchRecursive(arr, number, 0, arr.length - 1);
}
// 재귀적 이진 검색을 위한 도우미 함수
private static int binarySearchRecursive(int[] arr, int number, int left, int right) {
if (left > right) {
return -1; // 요소를 찾지 못한 경우
}
int mid = left + (right - left) / 2;
if (arr[mid] == number) {
return mid;
} else if (arr[mid] < number) {
return binarySearchRecursive(arr, number, mid + 1, right);
} else {
return binarySearchRecursive(arr, number, left, mid - 1);
}
}
public static void main(String[] args) {
int[] arr = {2, 4, 6, 8, 10, 12, 14, 16};
int number = 10;
int result = binarySearchRecursive(arr, number);
if (result != -1) {
System.out.println("요소가 인덱스에서 찾았습니다: " + result);
} else {
System.out.println("배열에서 요소를 찾지 못했습니다.");
}
}
}
반복문으로 구현한 이분 탐색
public class BinarySearch {
// 반복문을 이용한 이진 검색 함수
public static int binarySearchIterative(int[] arr, int number) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == number) {
return mid;
} else if (arr[mid] < number) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1; // 요소를 찾지 못한 경우
}
public static void main(String[] args) {
int[] arr = {2, 4, 6, 8, 10, 12, 14, 16};
int number = 10;
int result = binarySearchIterative(arr, number);
if (result != -1) {
System.out.println("요소가 인덱스에서 찾았습니다: " + result);
} else {
System.out.println("배열에서 요소를 찾지 못했습니다.");
}
}
}
자바 이분 탐색 라이브러리
꼭 직접 이분 탐색을 구현할 필요가 없다면 자바에서 기본으로 제공되는 이분 탐색을 쓰는 게 좋다.
자바 Arrays 클래스에 binarySearch란 함수가 이미 있다.

javadoc에도 나와있듯이 매개변수는 배열과 찾는 키, 또는 시작 인덱스와 끝 인덱스도 포함시켜 주면 된다. 그리고 만약에 찾는 수를 찾았을 때 그 키의 인덱스를 반환하고, 찾지 못하면 (-(insertion point) - 1을 반환한다. 이때, insertion point는 만약에 이 배열에 그 수를 넣었을 때의 인덱스이다.
이분 탐색 시간복잡도 및 빅오 표기
이분 탐색의 시간 복잡도는 O(log N)이다. log N인 이유는 크기가 N인 배열을 이분 탐색으로 원하는 수를 찾을 때 탐색 할 때마다 탐색 범위가 절반으로 줄어들기 때문이다.
따라서, 탐색 범위는 N, N / 2, N / 4, ... , 1이 된다.
처음부터 끝까지 원하는 값을 찾을 때까지 탐색을 계속하는 순차 탐색의 시간 복잡도는 O(n)이다. 따라서, 10만 개의 데이터가 있다면 무려 10만 번을 탐색해야 하는 것이다.
그러나, 이분 탐색은 탐색 대상을 절반씩 계속해서 줄여나가기 때문에, 탐색의 횟수가 log(100,000)이기 때문에 10만 개의 데이터가 있다고 하더라도 약 16번 정도로 탐색을 끝낼 수 있다.
'알고리즘' 카테고리의 다른 글
| [알고리즘] 계수 정렬 (Counting Sort) (0) | 2022.07.29 |
|---|---|
| [알고리즘] 병합 정렬 (Merge Sort) (0) | 2022.07.28 |
| [알고리즘] 퀵 정렬 (Quick Sort) (0) | 2022.07.25 |
| [알고리즘] 삽입 정렬 (Insertion Sort) (0) | 2022.07.21 |
| [알고리즘] 버블 정렬 (Bubble Sort) (0) | 2022.07.16 |




댓글