https://www.acmicpc.net/problem/9375
9375번: 패션왕 신해빈
첫 번째 테스트 케이스는 headgear에 해당하는 의상이 hat, turban이며 eyewear에 해당하는 의상이 sunglasses이므로 (hat), (turban), (sunglasses), (hat,sunglasses), (turban,sunglasses)로 총 5가지 이다.
www.acmicpc.net
- 문제
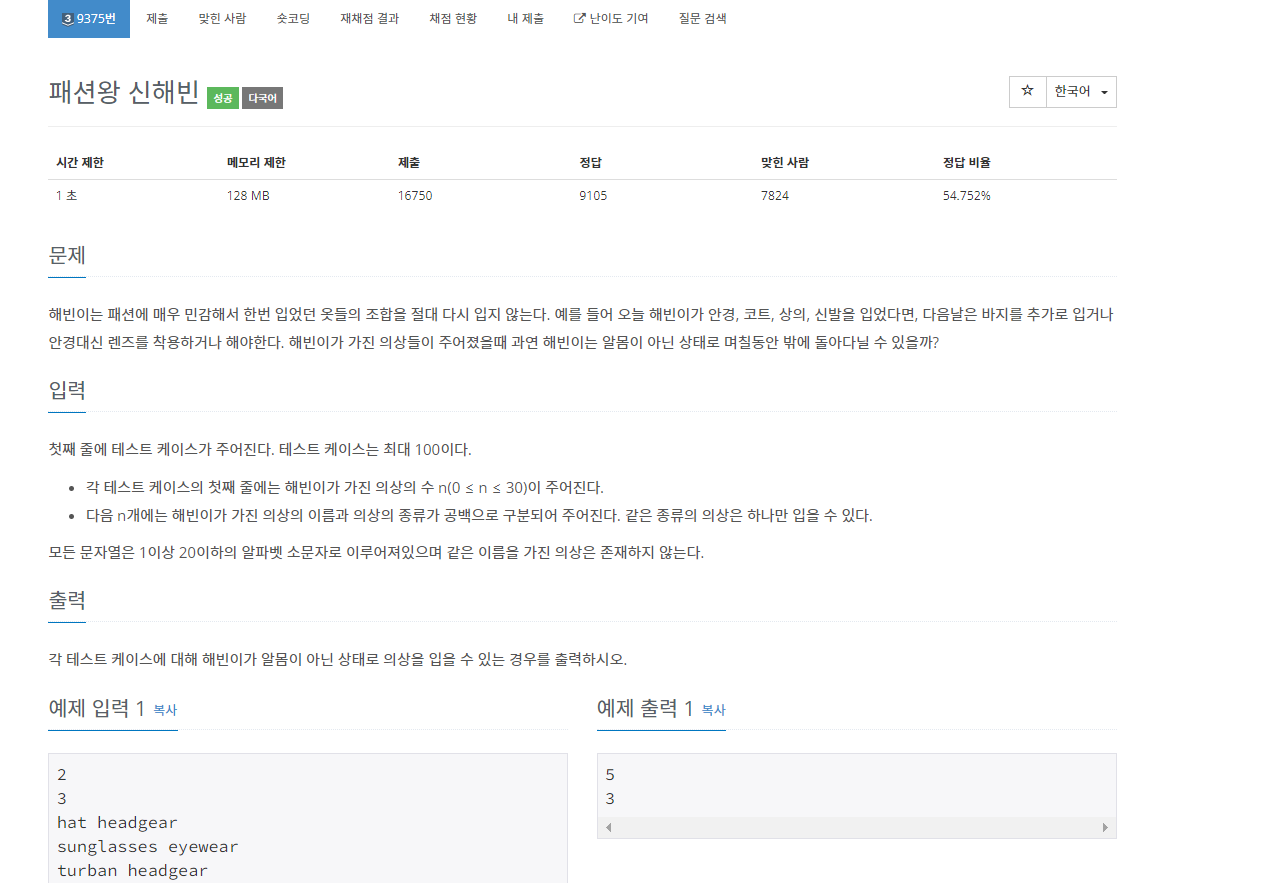
- 문제 풀이
백준 9375번 패션왕 신해빈은 실버 3 난이도의 수학 및 맵 문제이다. 이 문제에서는 의상의 종류들과 의상의 이름들이 주어진다. 한 종류는 겹쳐 입을 수가 없다. 이런 상황일 때 의상을 입을 수 있는 경우의 수를 구하는 문제이다.
우선 이 문제를 풀려면 공식을 구해야 한다. 일단 문제에서 주어진 예제들을 한번 보겠다.
EX 1) hat headgear, sunglasses eyewear, turban headgear
이 예시에는 2개의 의상의 종류가 있다. headgear와 eyewear가 있고 headgear에는 2개가 있다. 이 예시에는 다음과 같이 입을 수 있다 : (hat), (turban), (sunglasses), (hat, sunglasses), (turban, sunglasses). 따라서 총 5가지이다.
EX 2) mask face, sunglasses face, makeup face
이 예시에는 1개의 의상 종류만 있다. 따라서 3개의 경우의 수가 나온다. (mask), (sunglasses), (makeup)으로 총 3가지이다.
이처럼 옷의 한 종류를 하나를 골라 입거나 아니면 입지 않거나 하는 경우가 나온다. 때문에, 경우의 수를 셀 때 단순 개수의 곱이 아닌 입지 않는 경우를 고려하여 + 1을 한 결과를 곱셈해주어야 한다.
따라서 (옷의 종류당 개수 + 1) 들의 곱셈으로 구할 수 있는데, 옷을 하나도 입지 않으면 안 되기 때문에 옷을 하나도 입지 않는 경우를 - 1 처리하면 된다.
- 코드
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int t = Integer.parseInt(br.readLine());
for (int z = 0; z < t; z++) {
int n = Integer.parseInt(br.readLine());
Map<String, Integer> map = new HashMap<>();
for (int i = 0; i < n; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
st.nextToken();
String key = st.nextToken();
map.put(key, map.getOrDefault(key, 0) + 1);
}
int count = 1;
for (Map.Entry<String, Integer> entry : map.entrySet()) {
count = count * (entry.getValue()+1);
}
sb.append(count-1 + "\n");
}
System.out.print(sb);
}
}
- 후기
조합론 문제들을 많이 안 풀어봐서 그런지 나한테는 조금 어려웠던 문제였다. 앞으로 조합론 문제들을 차근차근 풀어봐야 될 거 같다.
'백준' 카테고리의 다른 글
| [백준] 2455번 : 지능형 기차 – JAVA [자바] (0) | 2022.04.26 |
|---|---|
| [백준] 2443번 : 별 찍기 - 6 – JAVA [자바] (1) | 2022.04.26 |
| [백준] 4358번 : 생태학 – JAVA [자바] (0) | 2022.04.26 |
| [백준] 1269번 : 대칭 차집합 – JAVA [자바] (0) | 2022.04.26 |
| [백준] 14425번 : 문자열 집합 – JAVA [자바] (1) | 2022.04.26 |




댓글