목차
플로이드 와샬이란?
다익스트라 알고리즘은 하나의 노드에서 출발했을 때 다른 모든 노드로의 최단 경로를 구하는 알고리즘이다. 하지만 플로이드 와샬 알고리즘은 모든 노드에서 모든 노드로의 최단 경로를 구하는 알고리즘이다. 그리고 다익스트라 알고리즘은 가장 적은 비용을 하나씩 선택을 해서 그 적은 비용을 가지는 노드의 인접한 노드들로 가는 비용을 하나씩 계산하는 방식이었다면 플로이드 와샬 같은 경우는 거쳐가는 노드를 기준으로 알고리즘을 수행한다는 특징이 있다. 추가로 플로이드 와샬은 다이나믹 프로그래밍 기법을 사용한 알고리즘이고, 인접 행렬을 이용하여 각 노드 간 최소의 비용을 계산한다.
플로이드 와샬 예시

위와 같은 그래프가 있다고 가정해 보겠다. 그리고 각각의 노드에서 다른 노드로 가는 비용을 2차원 배열로 나타내면 다음과 같다.
이 2차원 배열에서 INF는 무한, 즉 현재 노드에서 그 노드까지 바로 못 가는 것을 뜻한다. 그리고 n행 m열은 n번째 노드에서 m번째 노드로 가는 최소 비용을 뜻한다.
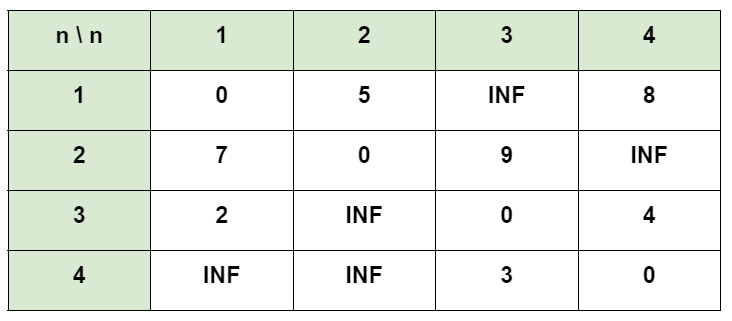
이 테이블은 현재까지 계산된 최소 비용을 뜻한다. 지금은 위에 있는 그래프의 상태를 테이블로 표시한 거와 같다. 이제 거쳐가는 노드를 보면서 반복적으로 이 테이블을 갱신해서 모든 최소 비용을 구해야 한다. 우선 노드 1을 거쳐가는 경우 먼저 살펴보겠다.
1. 노드 1을 거쳐가는 경우
노드 1을 거쳐가는 경우, 노란색으로 색칠되어 있는 부분들이 새로 갱신될 수 있는 비용들이다. 노란색으로 색칠되어 있는 것은 노드 1이 포함되지 않은 경우들이다.
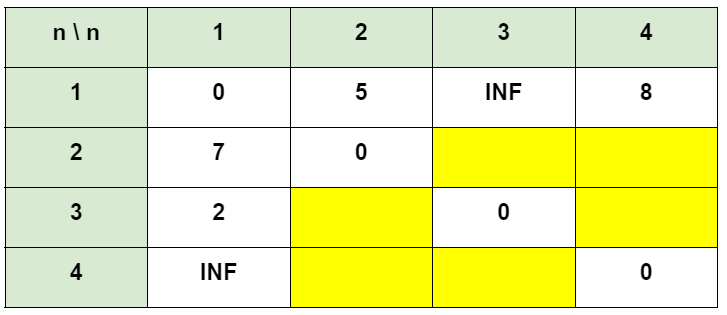
갱신은 X에서 Y로 가는 최소 비용과 X에서 노드 1로 가는 비용 + 노드 1에서 Y로 가는 비용을 비교해서 더 적은 비용으로 갱신하면 된다.
한번 예로 2에서 4로 가는 경우를 보겠다. 2번째 노드에서 4번째 노드로 가는 비용은 기존에는 INF, 즉 바로 가는 경우가 없었다. 하지만 노드 2에서 1로 가는 경우는 7이고 1에서 4로 가는 경우는 8로 총비용은 15이다. 15가 INF보다 적으니 2에서 4로 가는 경우를 15로 갱신해준다. 이런 방식으로 나머지들도 갱신해주면 다음과 같은 테이블이 나온다.

2. 노드 2를 거쳐가는 경우
노드 2를 거쳐가는 경우는 밑에 있는 테이블에서 노란색으로 색칠되어 있는 부분만 계산하고 더 적은 비용으로 갱신해주면 된다.

더 적은 비용으로 갱신했을 때 다음과 같은 결과를 구할 수 있다.

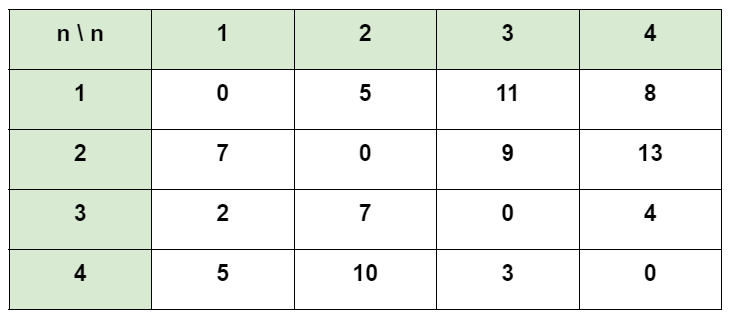
이제 위와 똑같은 방식으로 노드 3과 노드 4도 마찬가지로 계산을 하고 더 적은 비용으로 갱신을 하면 밑에 있는 최종 결과를 구할 수 있다.
코드
public class Main {
static int number = 4; //노드의 개수
static int INF = 1000000000; //무한
static int[][] arr = { //자료 배열 초기화
{0, 5, INF, 8},
{7, 0, 9, INF},
{2, INF, 0, 4},
{INF, INF, 3, 0},
};
// 플로이드 와샬 함수
static void floydWarshall() {
int[][] graph = new int[number][number];
for (int i = 0; i < number; i++) {
for (int j = 0; j < number; j++) {
graph[i][j] = arr[i][j];
}
}
for (int k = 0; k < number; k++) { // k = 거쳐가는 노드
for (int i = 0; i < number; i++) { // i = 출발 노드
for (int j = 0; j < number; j++) { // j = 도착 노드
if (graph[i][k] + graph[k][j] < graph[i][j]) {
// 노드 k를 거쳐가는 비용이 더 적으면 이 비용으로 갱신
graph[i][j] = graph[i][k] + graph[k][j];
}
}
}
}
}
}
시간 복잡도
이 알고리즘의 시간 복잡도는 O(n^3)이다. n은 노드 개수를 뜻한다.
'알고리즘' 카테고리의 다른 글
| [알고리즘] 다익스트라 (Dijkstra) (0) | 2022.05.25 |
|---|---|
| [알고리즘] DFS & BFS (0) | 2022.05.23 |
| [알고리즘] 배낭 문제 (Knapsack Problem) (0) | 2022.04.07 |
| [알고리즘] LIS (최장 증가 부분 수열) (1) | 2022.03.31 |
| [알고리즘] 큰 숫자 (정수) BigInteger 사용법 - JAVA [자바] (0) | 2022.03.27 |




댓글