목차
배낭 문제란?
배낭 문제란 담을 수 있는 최대 무게가 정해진 배낭이 있고 각각의 무게와 가치가 주어진 물건들이 주어졌을 때, 배낭에 담은 물건들의 가치가 최대가 되도록 하게 물건을 고르는 방법을 찾는 문제이다.
배낭 문제 예시
4가지의 물건 ABCD가 있고 배낭의 최대 무게는 5라고 가정하겠다.

무게가 1, 가치가 30인 물건을 A; 무게가 2, 가치가 20인 물건을 B; 무게가 3, 가치가 40인 물건을 C; 그리고 무게가 4, 가치가 10인 물건을 D라고 하겠다. 그리고 우리가 가진 가방의 최대 무게는 5이다. 이때 이 가방에 넣을 수 있는 최대 가치가 몇인지를 구하는 것이다.
예를 들어서 B와 C를 넣어서 총가치가 60이 되도록 가방에 넣을 수 있고, 아니면 A와 D를 넣어서 총가치가 40이 되도록 가방에 넣을 수 있다. 배낭 문제에서는 조합을 다양하게 할 수 있고 우리는 가방에 최대 가치를 넣을 수 있는 방법을 찾으면 된다.
방법 1 : 브루트 포스 (Brute-Force)
먼저 떠오르는 방법은 브루트 포스이다. 브루트 포스란 조합 가능한 모든 물건들을 하나씩 조합해 보는 방식이다.
배낭 문제에서 브루트 포스는 아주 간단하다. 각각의 물건이 들어있는 경우, 들어있지 않은 경우로 나눌 수 있다. T가 물건이 들어있는 경우, F가 물건이 없는 경우라고 하겠다.

즉, A가 들어있는 케이스, A가 들어있지 않은 케이스, 그리고 B가 들어있는 케이스, B가 들어있지 않은 케이스로 나눌 수 있다. 이러면 물건이 4개가 있을 때 총 2^4 가지의 방법이 있고 물건의 개수가 n이면 2^n 가지의 방법이 있다. 이러면 시간 복잡도가 O(2^n)이 되어서 너무 느리므로 DP로 해결해야 한다.
방법 2 : 다이나믹 프로그래밍 (DP)
DP는 큰 문제를 작은 문제로 쪼개서 푸는 방법이다. DP로 해결하려면 각각의 물건이 있는지 없는지를 생각해야 한다.
위에서 소개한 문제처럼 물건 ABCD가 있고 무게 제한이 5인 배낭 문제를 다음과 같이 표시하겠다
NS ("ABCD", 5)
우선 마지막 물건 D가 가방에 있는 경우, 없는 경우로 나눌 수 있다.
즉, D가 있는 경우 NS(ABC, 1) + 10 (D가 있어서 배낭의 무게 제한은 1이 되고 가치 10을 더한다) 그리고 D가 가방에 없는 경우 NS(ABC, 5) + 0으로 나눌 수 있다.
그림으로 표시하면 다음과 같다.

이 경우에서 이제 물건 C가 있는 경우, C가 없는 경우로 또 나눌 수 있다. 마찬가지로 하면 다음과 같이 나타낼 수 있다.
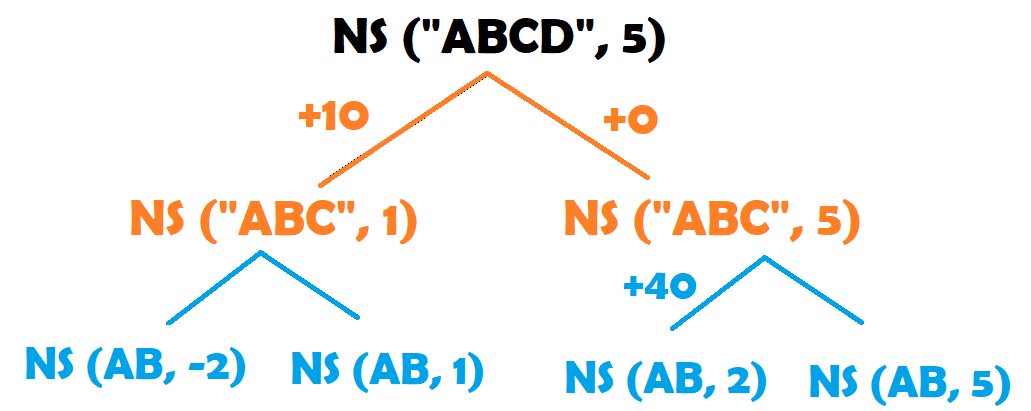
하지만 무게가 음수가 될 수는 없으므로 첫 경우는 지운다. 그리고 이렇게 물건 A와 물건 B를 마찬가지로 해준다.
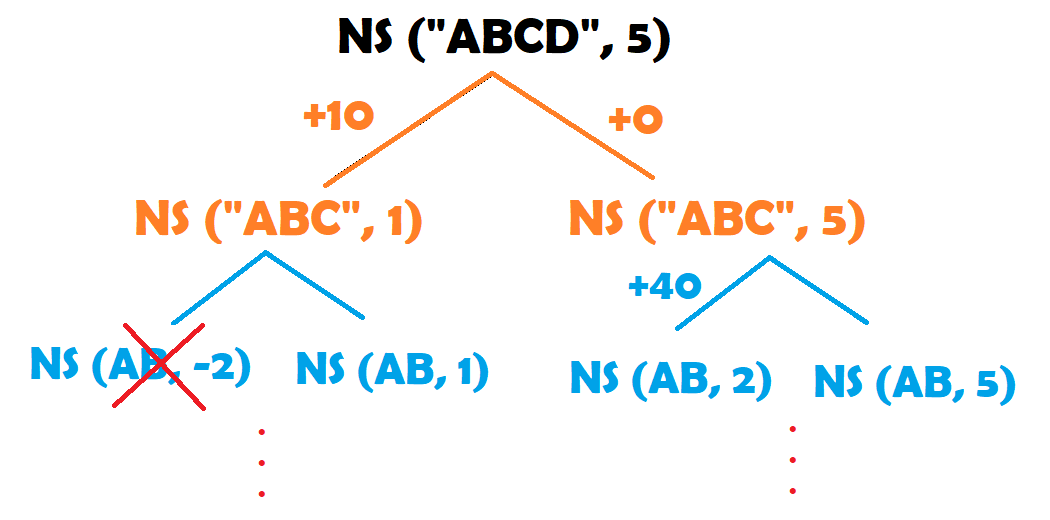
이를 점화식으로 나타낼 수 있다. 배낭 문제의 점화식은 어떠한 무게 제한이 있을 때 가방의 최대 가치를 나타내는 것이다.

N : 물건들의 개수
W : 현재 상태의 무게 제한
NS (N-1, W - W [n]) + val [n] : n번째 물건을 배낭에 넣은 경우. 해당 물건을 넣었기 때문에 기존 무게에서 n번째 물건의 무게를 빼줘야 한다. 그리고 n번째 물건의 가치를 더해야 하므로 val [n]을 더한다.
NS (N-1, W) : n번째 물건이 없는 경우. 배낭에 물건을 추가하지 않았기 때문에 무게 W는 그대로이다.
이 점화식에는 변수가 N, W, 총 2가지 이므로 2차원 DP 테이블을 만들어서 해결한다.
세로축이 N, 가로 측이 W를 나타낸다. 우리는 이 예제에서 물건 ABCD 4개가 있고 무게 제한이 5이므로 NS (4, 5)를 구해야 한다. 즉 밑에 있는 테이블에서 빨간색으로 표시되어있는 공간을 구해야 한다.
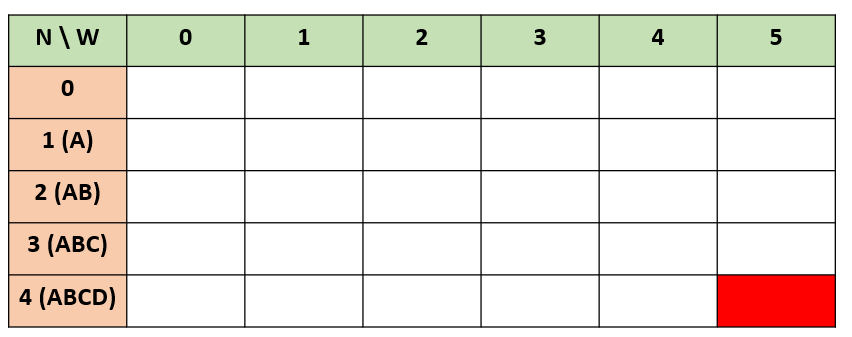
우선 N = 0일 때, 즉 배낭에 물건을 하나도 안 넣으면 가치가 0이다. 추가로, W = 0일 때, 즉 배낭의 무게 제한이 0이면 배낭에 물건을 하나도 넣을 수 없으므로 가치는 0이다. 따라서 테이블에 다음과 같이 표시할 수 있다.

첫 번째 경우는 물건 A가 있는 경우와 A가 없는 경우로 나눌 수 있다. 무게 1을 가진 물건 A는 대각선 방향으로 가는 경우, 즉 물건 A가 있는 경우와 세로 방향으로 가는 경우, 즉 물건 A가 없는 경우가 있다. 대각선으로 가면 가치 30이 더해지고 세로로 내려오면 가치가 더해지지 않는다. 그리고 각각의 경우에서 맥시멈, 즉 더 큰 값을 고르면 된다. 따라서 N이 1일 때 가치는 30이 된다.
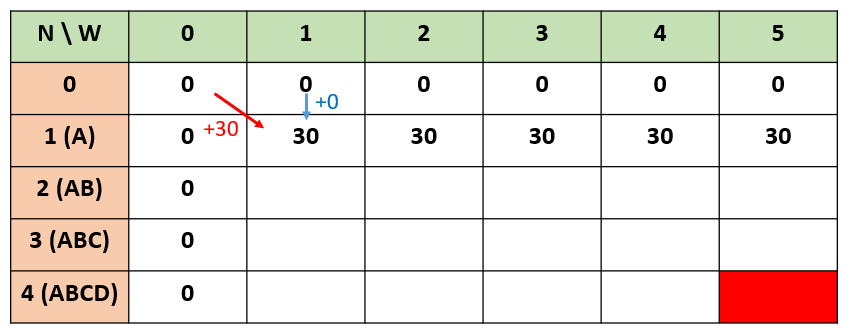
두 번째는 B가 있는 경우와 B가 없는 경우로 나눌 수 있다. B를 배낭에 넣을 수 없는 경우는 위에서 세로로 내려오고 B를 배낭에 넣을 수 있는 경우는 대각선으로 오면서 W가 2만큼 더해지고 가치가 20이 더해진다.
N = 2, W = 1일 때는 B를 배낭에 넣을 수 없다. 즉, 위에서 세로로 내려오기 때문에 N = 2, W = 1일 때의 가치는 30이다.
N = 2, W = 2일 때 B를 배낭에 넣으면 무게가 2만큼 더해지므로 N = 1, W = 0에서 20을 더할 수 있고 아니면 N = 1, W = 2에서 세로로 내려오면 된다. 이 두 경우에서 더 큰 값, 즉 30을 택한다.
N = 2, W = 3일 때 N = 1, W = 1에서 W를 2만큼 더하면서 가치를 20만큼 더 할 수 있으므로 가치가 50이 된다. 이것은 W가 4, 5일 때도 마찬가지이다. 따라서 다음과 같이 테이블을 채울 수 있다.
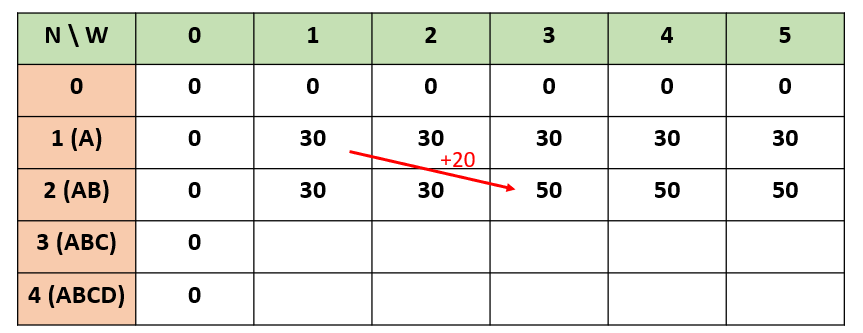
세 번째 물건 C도 마찬가지로 해주면 된다. C의 무게가 3이므로 W = 1, 2일 때의 최댓값은 그래도 30 (A를 배낭에 넣었을 때)이다.
W = 3일 때 : N = 2, W = 0에서 C를 넣으면 배낭의 가치가 40이 된다. 하지만 A와 B를 넣으면 가치가 50이 되므로 W = 3일 때 배낭의 가치는 50이다.
W = 4일 때 : N = 2, W = 1은 30이고 여기서 C를 넣으면 가치가 70이 되므로 최대 가치는 70이 된다.
W = 5일 때 : W = 4일 때와 같다.

D의 무게가 4이므로 W = 1 ~ 3일 때는 N = 3일 때와 같다.
NS (4,4) = max(NS (3, 1) + 10, NS (3, 4)) = max(40, 70) = 70.
NS (4,5) = max(NS (3, 2) + 10, NS (3, 5)) = max(40, 70) = 70.
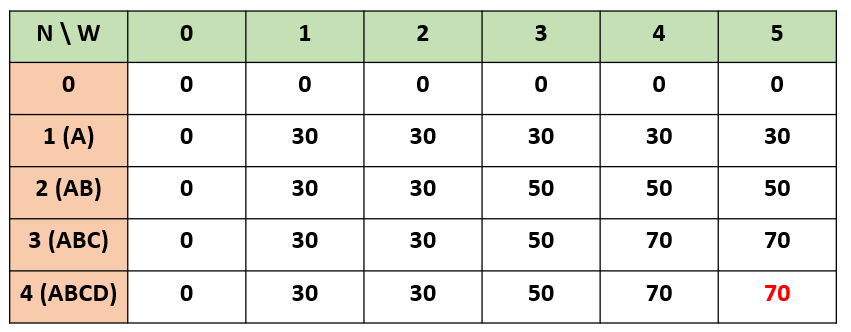
따라서 이 예제의 답은 70이 된다. A와 C를 넣었을 때 배낭의 가치는 70이 된다.
이렇게 DP로 배낭 문제를 해결하면 시간 복잡도는 O(N·W)가 된다.
코드
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken()); //물건 개수
int k = Integer.parseInt(st.nextToken()); //최대 무게
int[][] dp = new int[n+1][k+1];
int[] w = new int[n+1]; //물건의 무게들
int[] v = new int[n+1]; //물건의 가치들
for (int i = 1; i <= n; i++) {
st = new StringTokenizer(br.readLine());
w[i] = Integer.parseInt(st.nextToken());
v[i] = Integer.parseInt(st.nextToken());
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= k; j++) {
if (w[i] <= j) {
dp[i][j] = Math.max(dp[i-1][j-w[i]]+v[i], dp[i-1][j]);
} else {
dp[i][j] = dp[i-1][j];
}
}
}
System.out.print(dp[n][k]);
}
}
'알고리즘' 카테고리의 다른 글
| [알고리즘] DFS & BFS (0) | 2022.05.23 |
|---|---|
| [알고리즘] 플로이드 와샬 (Floyd Warshall) (2) | 2022.05.21 |
| [알고리즘] LIS (최장 증가 부분 수열) (1) | 2022.03.31 |
| [알고리즘] 큰 숫자 (정수) BigInteger 사용법 - JAVA [자바] (0) | 2022.03.27 |
| [알고리즘] LCS (최장 공통 부분 수열) (1) | 2022.01.30 |




댓글