목차
Learning Objectives
• Explain how function application works by substituting parameters for arguments
• Execute simple programs involving lambdas
• Explain what name shadowing and name capture is
• Implement recursion using only lambdas
• Explain how environments are delayed substitutions
Functions in Paret
Examples


Syntax (Lab/Extended)

Example


Example

Function Application
Parentheses around something is a function application (function call)
+, -, * are essentially built-in functions
→ 즉, let이나 lambda 같은게 괄호 안에 없으면 function application
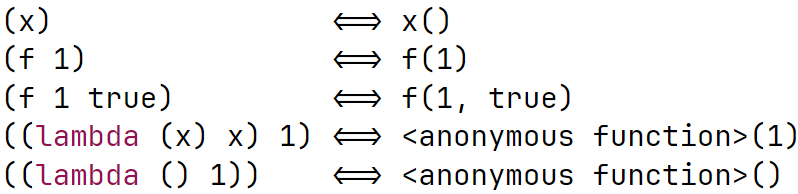
Recursion

It gives an error because to call a function, you need to have already defined it
Free variable/identifier : It does not have a binding it can refer to
Recursion by Feeding Functions Themselves

When calling the function, I first call the function itself and then I pass my extra arguments so by wrapping it, I can refer to the location.
이것도 가능.

Currying
Currying: Turning a multi-argument function into a single argument function.
The advantage of a curried function is that you can provide arguments one by one and construct partially applied functions, rather than having to provide them all at once.
Partial application: Providing a function with only some of its arguments, giving a new function for which only the remaining arguments must be provided.

Example in Paret

Why is currying useful?
Currying shows that single-argument lambdas are a simple core language for functions in general
Curried functions are convenient for when you want to partially apply a function with multiple arguments

What you want to do is create a new curried function where username and password are already set and just pass queries around.
Three ways to Curry add in Scala

→ add is a function that takes an integer x and returns another function that takes an integer y and returns the sum of x and y. This function is curried.
→ This line applies the argument 1 to the add function, resulting in a new function incByOne that adds 1 to its argument.
→ In this line, incByOne is applied to 2, which results in 3. So, 3 is assigned to three.
→ In this line, you can also directly apply both arguments at once to the add function, resulting in the value of 3. This is possible because the function add is curried, allowing you to either apply arguments partially or all at once.

→ add is defined as a function that takes an integer x and returns another function that takes an integer y and computes the sum of x and y.
→ This line partially applies the argument 1 to the add method, resulting in a new function incByOne that adds 1 to its argument.
→ Here, incByOne is applied to 2, resulting in 3, so 3 is assigned to three.
→ Again, you can apply both arguments at once to the add method, resulting in the same value of 3.

→ A regular function add that takes two integer arguments x and y and returns their sum.
→ Here, add.curried(1) partially applies the first argument 1 to the add function. It returns a new function that takes the second argument y, and when called, it adds 1 to y.
→ This line calls incByOne function with the argument 2, so 3 is assigned to three.
→ Here, you are directly calling the curried add function with both arguments 1 and 2, which results in 3.
Currying, more generally

Function Semantics

e [a / b] means: inside of expression e, substitute (replace) all instances of a with b
→ When you interpret a lambda, it has to become a value where we keep storing its parameter name and body without interpreting those because we don't know what's gonna come out of the function.
→ In the calling of a function, the first thing has to become a function value and the second thing is just interpreting the body, but we are going to substitute all parameters with the arguments.
Properties
Beta property: ( ( λ ( x ) e1 ) e2 ) ↔ e1[x / e2]
→ Function application defined via substitution
Beta-eta property: ( ( λ ( x ) e1 x ) e2 ) ↔ (e1 e2)
→ Function application works the same for all possible terms
→ No capturing of free variables
Substitution
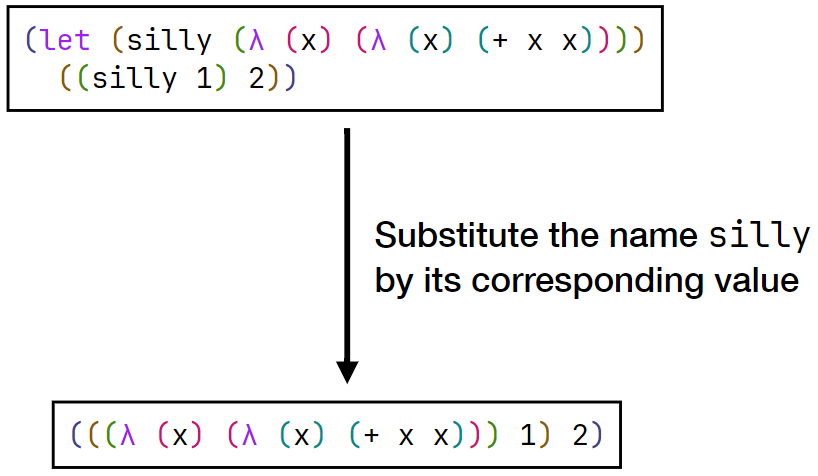
Substitution: Replacing a name with its corresponding name (expression).
A substitution-based interpreter would evaluate binding definitions (let or function applications) by directly replacing all occurrences of names referring to said definition in the sub-AST with their definition.
Example in Scala

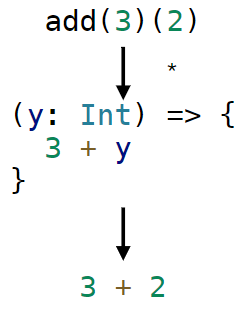
Example in Scala
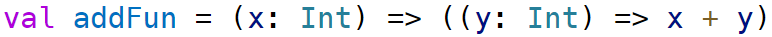

Example in Paret 1


Name Shadowing
Scala

silly(1)(2) → 4 (always refer to the closest variable)
Names always associate to binding that is lexically closest (i.e. closest in the program text)
Substitution should take this principle into account
Name Shadowing Java
Name Shadowing: when one binding hides another binding with the same name


Why shadowing matters: Why use the same variable twice? There are cases of using the same variable more than once e.g. in a library class
Name Shadowing Paret
You can always create a new value, even if the name was used before
→ Useful because Paret is immutable
→ Useful because everything in Paret is nested
→ Useful for e.g. libraries (overriding definitions)
Example

Name Capture
Name capture: When a free variable refers to the wrong binding (under static scoping), it is captured.
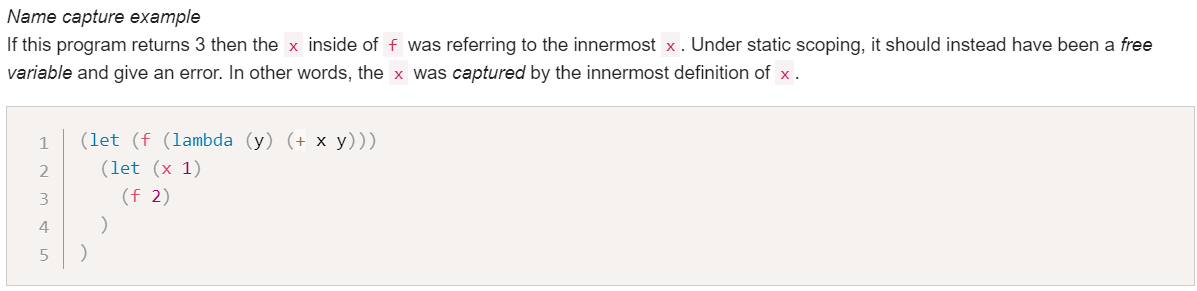
Free variables: variables that refers to nothing at its definition
Most languages disallow free variables
Capturing of Free Variables

Our free variable x was captured by the x binding coming from the let.
→ 여기서, 함수 선언할 때 x + y를 하는데, 이때 x가 선언되지 않은 상태임.
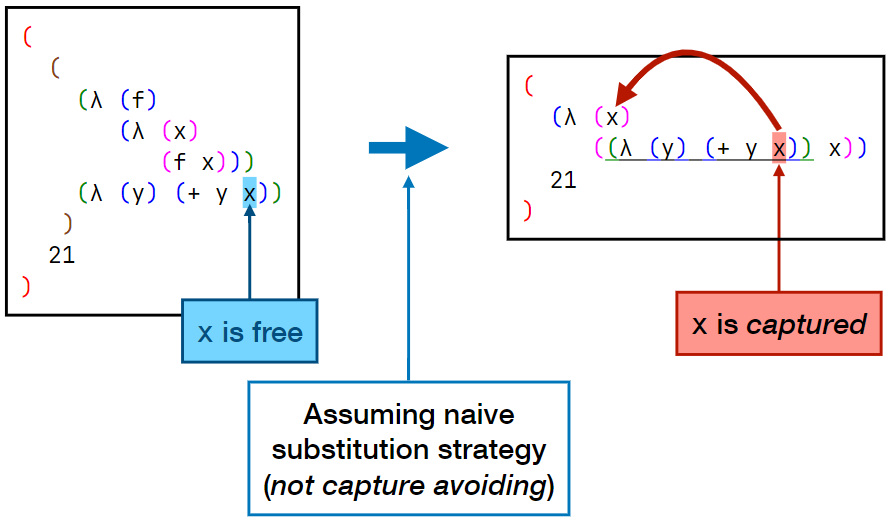
Avoiding Name Capture


Environments
Environments = delayed substitutions
Environments: A mapping from names to their corresponding meaning. By keeping track of binding definitions in an environment, the meaning of a name can be looked up when needed.
Binding
Bind = The following name will now represent this value, but only in a specific region, scope.
→ Variable, value, Function, Field, Method, class
Scope
Scope: The region where bindings are available
Example:

Static scoping (lexical scoping): The meaning of a name comes from the lexically closest definition. For functions, it means names refer to their closest definition at the definition site of the function.
Dynamic scoping: The meaning of a name is determined only by using the available names at the moment of evaluation (e.g. call site of functions). Few cases where languages use dynamic scoping, but it makes it easier to implement interpreters.

Environment
Environment: A way to store bindings
Idea: rather than directly substituting, always keep track of all names that are accessble and their corresponding values
We can look up values as needed
Advantage over substitution: Substitution has to pass over the AST to substitute, and has to substitute in parts that may never even be executed.
Example 1:

Example 2:
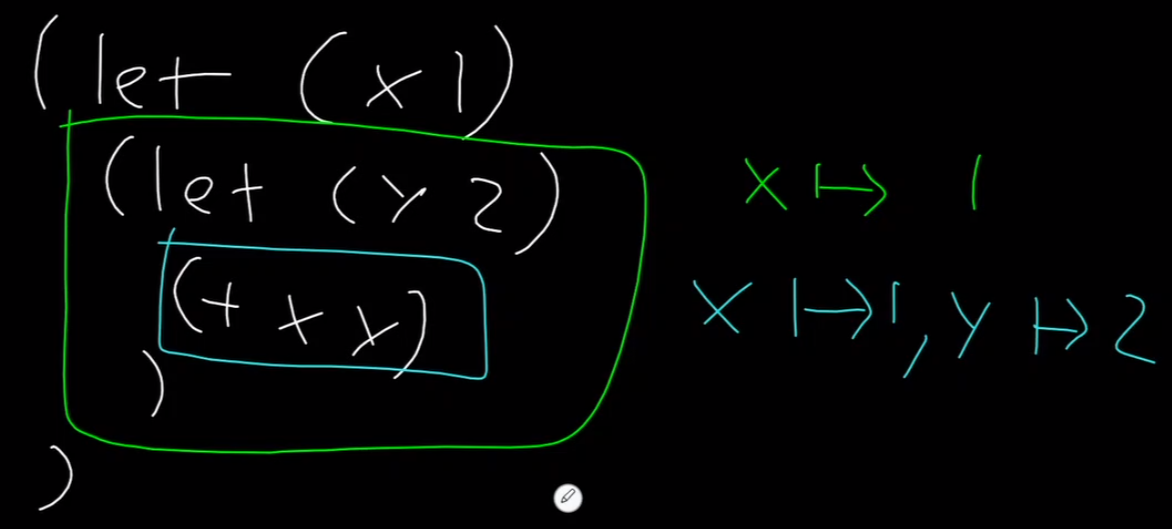
Making it simple in Paret
No mutation: values (constants) instead of variables

No forward Referencing:

Why allow this?
- Difficult to implement and already disallowed in most cases, even in Java
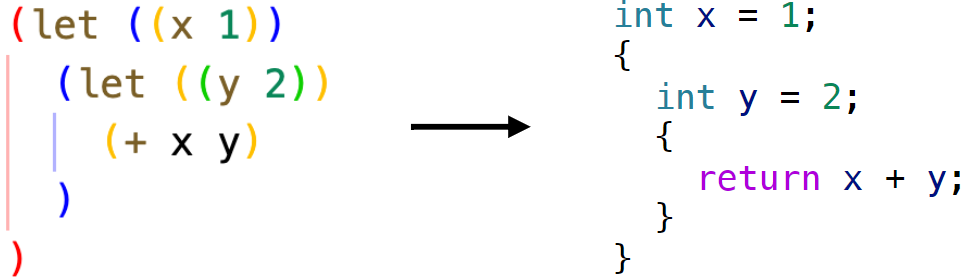
Nested structure of Paret enforces clear lexical scoping
Environments Example (Java):

[ ] empty environment in the beginning
Line 1: [calculate → ( ) => Int]
Line 2: [calculate → ( ) => Int, x → 1]
Line 3: [calculate → ( ) => Int, x → 1, y → 2]
Line 4 - 7 (inside the if statement): [calculate → ( ) => Int, x → 1, y → 2, z → 2], need to look up x and y in another environment
Line 9: (여기에 z가 있으면 cannot lookup this value), 가장 최근 environment인 line 3에 있는 값들, 따라서 need to keep track of the environments
Environments Example (Paret):

f will be added to the green region, but f cannot reference to the green region (forward referencing)
Closures
Closes under substitution
Scoping Rules
Bodies of functions (lambdas) have access to their parameters
Bodies of functions (lambdas) have access to bindings that are available when they are defined
Bodies of functions (lambdas) do not have access to bindings that are available when they are executed → This would be capturing

When we define a function, let's store what it had access to at that point. So rather than storing the function as a value with its (parameter, body), we are also going to store vwhatever it had access to when it got defined → Environment as it was when it was defined.
Why we need closures

y is free
f doesn't have access to anything (empty environment)
f → Closure

Semantics (Environments)
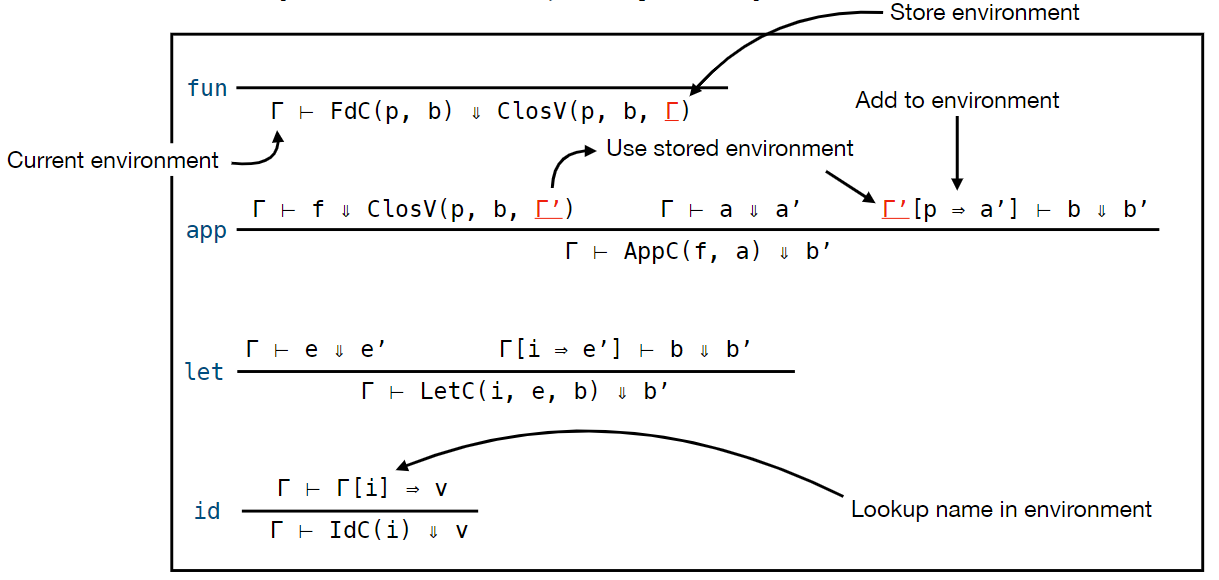
TEXTBOOK NOTES
Function Application:
FdC(params: List[String], body: ExprC)
AppC(f : ExprC, args: List[ExprC])
여기서 params는 함수의 parameter들. Body는 함수에서 해야하는거.
Function Application:
1. Look up the function definition (f)
2. Evaluate its body
'학교 > CPL' 카테고리의 다른 글
| CPL 3: Function Interpretation and Environments (0) | 2024.03.31 |
|---|---|
| Lecture 6: Environments and Scoping (0) | 2024.03.29 |
| CPL 2-3: Higher Order Functions (1) | 2024.03.27 |
| Lecture 4: Functions (1) | 2024.03.27 |
| CPL 1-2: Semantics and Transformations (0) | 2024.03.26 |




댓글