https://www.acmicpc.net/problem/11502
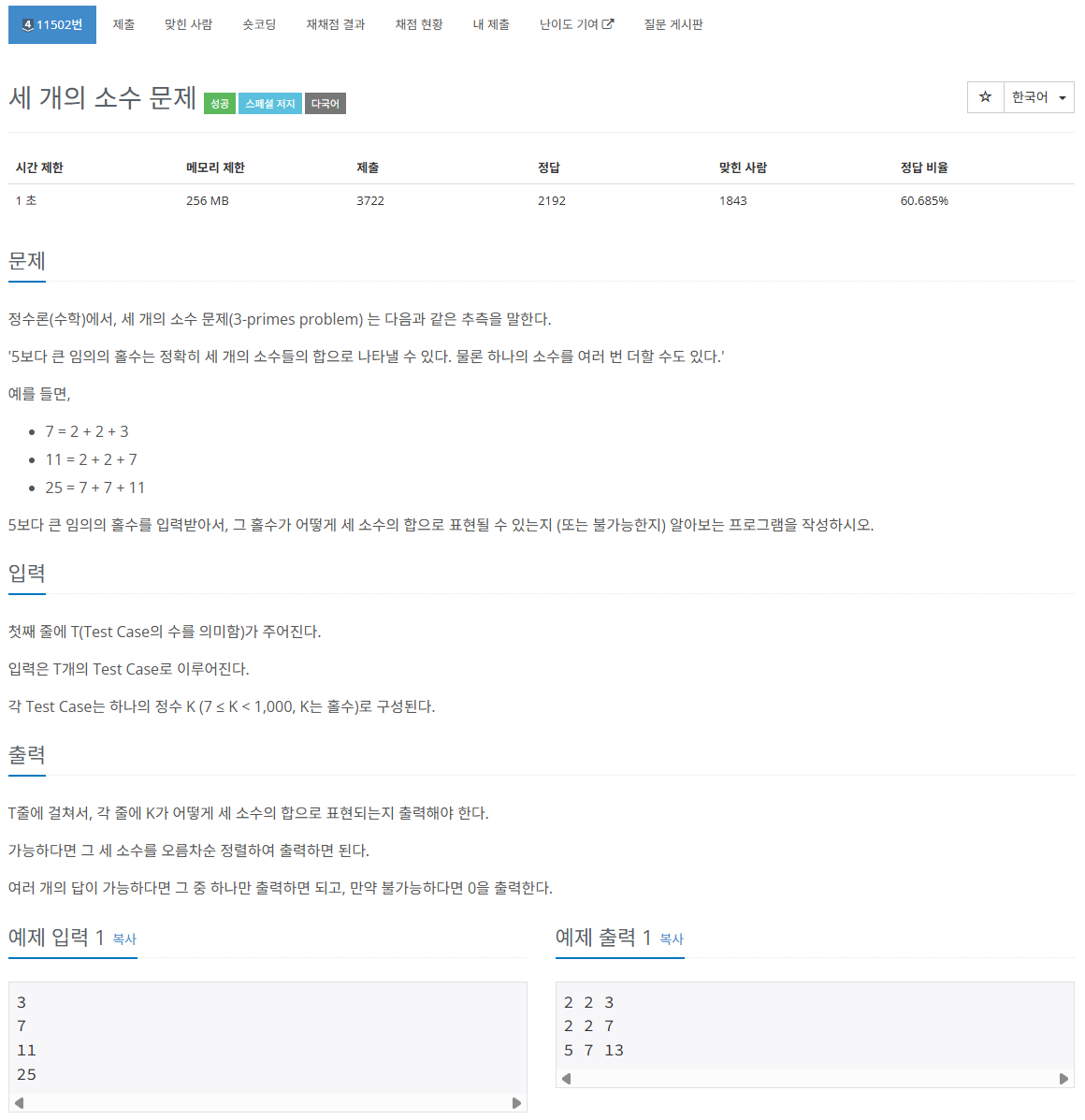
문제
해결 방법
이 문제를 해결하기 위해 다음과 같은 접근 방식을 사용한다.
1. 소수 목록 생성
- 7부터 999까지의 홀수 중 소수들을 미리 구해놓는다.
- 에라토스테네스의 체를 사용하여 빠르게 소수를 판별한다. 에라토스테네스의 체의 대한 자세한 정보는 여기서 확인할 수 있다.
2. 세 개의 소수로 표현 가능한지 확인
- 세 개의 소수를 더해서 K가 되는 조합을 찾는다.
- 오름차순 정렬된 결과를 출력한다.
- 여러 답이 있을 경우, 발견한 첫 번째 조합을 출력한다.
- 불가능한 경우 0을 출력한다.
이제 이를 바탕으로 코드 구현을 진행한다.
코드
import java.io.*;
import java.util.*;
public class Main {
static List<Integer> primes;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int t = Integer.parseInt(br.readLine());
getPrimes();
StringBuilder sb = new StringBuilder();
for (int i = 0; i < t; i++) {
sb.append(getThreePrimes(Integer.parseInt(br.readLine()))).append("\n");
}
System.out.print(sb);
}
// 에라토스테네스의 체를 이용하여 소수 목록 생성
public static void getPrimes() {
boolean[] isPrime = new boolean[1001];
primes = new ArrayList<>();
for (int i = 2; i <= 1000; i++) {
if (!isPrime[i]) {
primes.add(i);
for (int j = i * 2; j <= 1000; j += i) {
isPrime[j] = true;
}
}
}
}
// 주어진 수를 세 개의 소수 합으로 표현
public static String getThreePrimes(int n) {
for (int i = 0; i < primes.size(); i++) {
if (primes.get(i) > n) return "0";
for (int j = i; j < primes.size(); j++) {
for (int k = j; k < primes.size(); k++) {
if (primes.get(i) + primes.get(j) + primes.get(k) == n) {
return primes.get(i) + " " + primes.get(j) + " " + primes.get(k);
}
}
}
}
return "0";
}
}
코드 설명
1. 소수 리스트 생성 (getPrimes)
- boolean [] isPrime을 활용해 에라토스테네스의 체 방식으로 1000 이하의 소수를 미리 계산한다.
- primes 리스트에 소수를 저장하여 사용한다.
2. 세 개의 소수 합으로 표현 (getThreePrimes)
- primes 리스트를 순회하며 i, j, k를 선택하여 n과 일치하는 조합을 찾는다.
- 중복된 조합을 방지하기 위해 i ≤ j ≤ k 조건을 유지하여 탐색한다.
- 찾은 조합을 문자열로 반환하여 출력한다.
- 존재하지 않으면 "0"을 반환한다.
시간 복잡도 분석
1. 소수 리스트 생성 (getPrimes)
- 에라토스테네스의 체: O(N log log N) → 1000 이하의 수에 대해 매우 빠르게 실행됨.
2. 세 개의 소수 합 찾기 (getThreePrimes)
- primes 리스트 크기는 대략 168개 (2부터 1000까지의 소수 개수)
- 세 중첩 반복문: O(P^3)
따라서 전체 과정의 시간 복잡도는 O(N log log N) + O(P^3)가 된다.
'백준' 카테고리의 다른 글
| [백준] 1990번 : 소수인팰린드롬 – JAVA [자바] (0) | 2025.03.19 |
|---|---|
| [백준] 2075번 : N번째 큰 수 – JAVA [자바] (0) | 2025.03.18 |
| [백준] 1124번 : 언더프라임 – JAVA [자바] (0) | 2025.03.17 |
| [백준] 1145번 : 적어도 대부분의 배수 – JAVA [자바] (0) | 2025.03.14 |
| [백준] 12852번 : 1로 만들기 2 – JAVA [자바] (0) | 2025.03.14 |




댓글