https://www.acmicpc.net/problem/11053
11053번: 가장 긴 증가하는 부분 수열
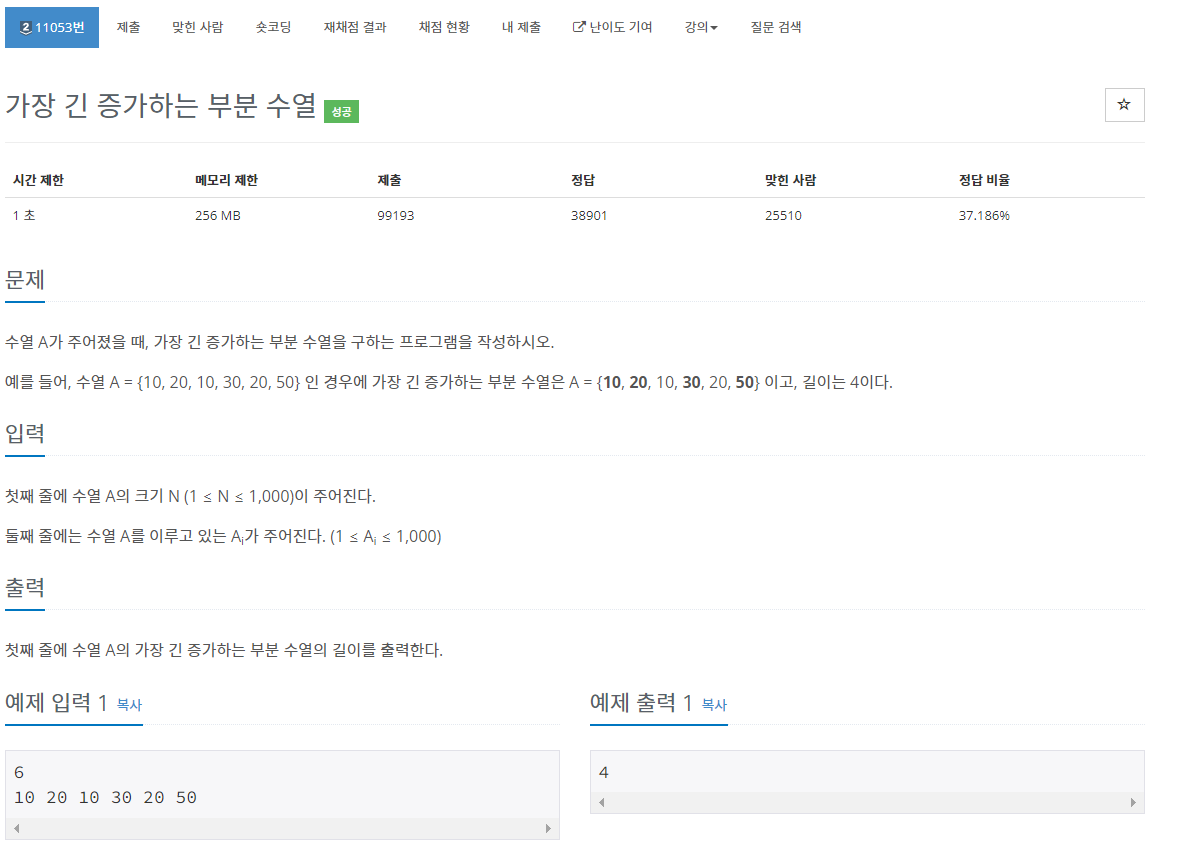
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오. 예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이
www.acmicpc.net
- 문제
- 문제 풀이
백준 11053번 가장 긴 증가하는 부분 수열은 DP 문제, 그중에서도 LIS를 이용해서 푸는 문제이다. LIS를 공부하고 싶으면 밑에 있는 링크를 참고하면 되겠다.
※참고※
https://propercoding.tistory.com/41
[알고리즘] LIS (최장 증가 부분 수열)
목차 LIS란? LIS는 Longest Increasing Subsequence의 약자이다. 말 그대로 최장 증가 부분 수열, 또는 가장 긴 증가하는 부분 수열이라고 불린다. LIS는 주어진 수열에서 오름차순으로 정렬된 가장 긴 부
propercoding.tistory.com
문제에서 주어진 예제를 한번 보겠다.
문제에서 주어진 수열은 arr = {10, 20, 10, 30, 20, 50}이다.

처음 dp 값은 1로 시작한다.

현재 값은 20이고 20보다 작거나 같은 이전 원소들 중 가장 큰 dp값이 1이므로 (Arr이 10일 때) 1+1 = 2를 현재 dp값으로 저장한다.

현재 값이 10이고 10보다 작거나 같은 이전 원소들 중 가장 큰 dp값이 1이므로 (Arr이 10일 때) 1 + 1 = 2를 현재 dp값으로 저장한다.

현재 값이 30이고 30보다 작거나 같은 이전 원소들 중 가장 큰 dp 값이 2이므로 (Arr이 20일 때, 혹은 10일 때) 2 + 1 = 3을 현재 dp값으로 저장한다.

현재 값이 20이고 20보다 작거나 같은 이전 원소들 중 가장 큰 dp 값이 2이므로 2 + 1 = 3을 현재 dp값으로 저장한다.

마지막 값이 50이고 50보다 작거나 같은 이전 원소들 중 가장 큰 dp 값이 3이므로 3 + 1 = 4를 현재 dp값으로 저장한다. 따라서 수열 Arr의 LIS 길이는 4이다.
- 코드
import java.io.*;
import java.util.*;
public class Main{
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine()); //수열 arr의 길이
int[] arr = new int[n+1]; //수열 배열 초기화
int[] dp = new int[n+1]; //dp 테이블 초기화
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 1; i <= n; i++) {
arr[i] = Integer.parseInt(st.nextToken()); //arr에 수열 입력 받기
dp[i] = 1; //모든 dp값들은 최소 1
}
int max = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j < i; j++) {
if (arr[i] > arr[j]) dp[i] = Math.max(dp[i], dp[j]+1);
// 이전 원소들 중 가장 큰 dp값 + 1
}
max = Math.max(max, dp[i]); //LIS 길이 구하기
}
System.out.print(max);
}
}
- 후기
백준 11053번은 LIS의 기본 문제이니 확실하게 이해하고 풀 줄 알아야 되는 문제인 거 같다.
'백준' 카테고리의 다른 글
| [백준] 7861번 : Longest Ordered Subsequence – JAVA [자바] (0) | 2022.04.01 |
|---|---|
| [백준] 17216번 : 가장 큰 감소 부분 수열 – JAVA [자바] (0) | 2022.03.31 |
| [백준] 11060번 : 점프 점프 – JAVA [자바] (0) | 2022.03.30 |
| [백준] 14495번 : 피보나치 비스무리한 수열 – JAVA [자바] (0) | 2022.03.29 |
| [백준] 9658번 : 돌 게임 4 – JAVA [자바] (0) | 2022.03.28 |




댓글