https://www.acmicpc.net/problem/2293
2293번: 동전 1
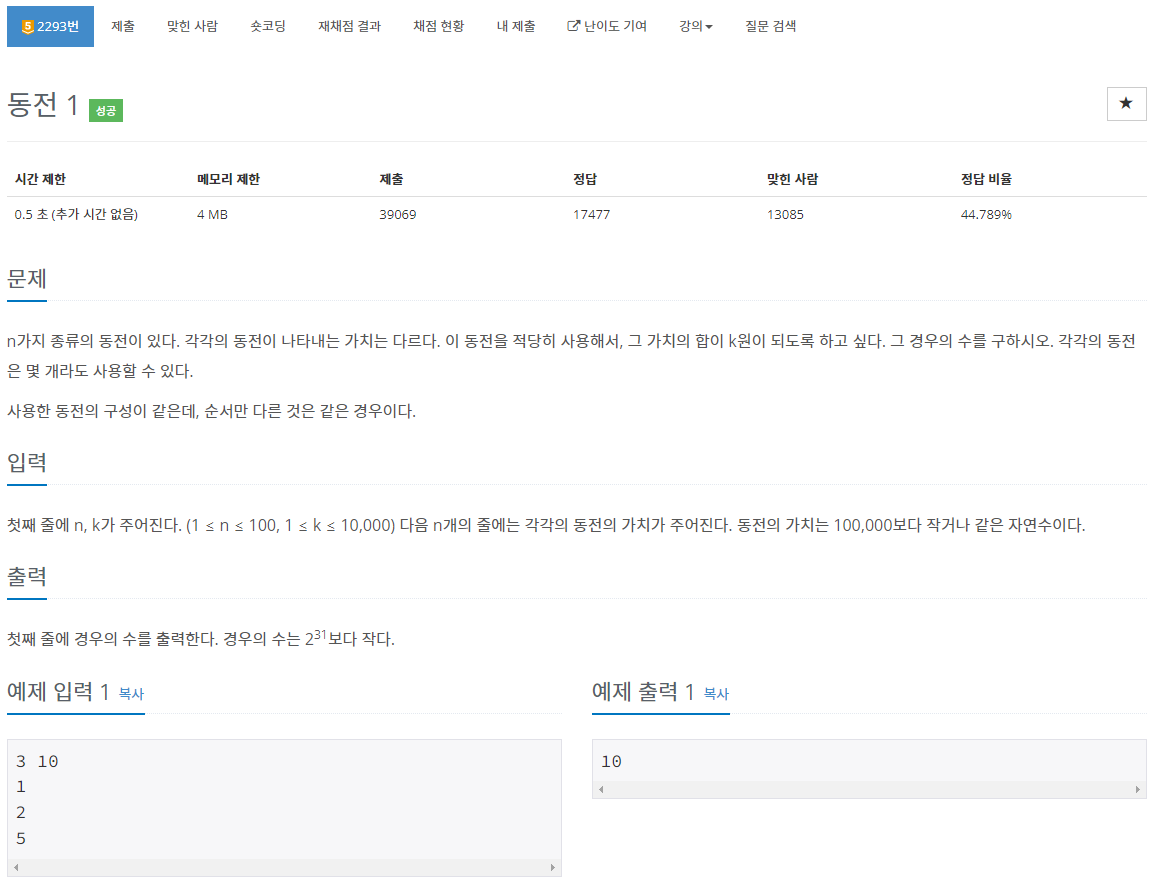
첫째 줄에 n, k가 주어진다. (1 ≤ n ≤ 100, 1 ≤ k ≤ 10,000) 다음 n개의 줄에는 각각의 동전의 가치가 주어진다. 동전의 가치는 100,000보다 작거나 같은 자연수이다.
www.acmicpc.net
- 문제
- 문제 풀이
백준 2293번은 골드 5 난이도의 DP (다이내믹 프로그래밍) 문제다. 만약에 DP 이론을 공부하고 싶으면 밑에 있는 링크를 참고하면 되겠다.
https://propercoding.tistory.com/entry/알고리즘-다이내믹-프로그래밍-Dynamic-Programming
[알고리즘] 다이나믹 프로그래밍 (Dynamic Programming)
목차 다이나믹 프로그래밍이란? 다이나믹 프로그래밍 (Dynamic Programming) 또는 동적 계획법은 큰 문제를 작은 문제로 쪼개서 푸는 기법이다. 다이나믹 프로그래밍의 특징은 모든 작은 문제들은 단
propercoding.tistory.com
이 문제에는 n가지의 동전이 있고 이 n가지의 동전을 써서 k원이 되게 하는 경우의 수를 출력하면 되는 문제이다. 그리고 이 문제에는 메모리 제한이 4MB로 되게 낮다. 따라서 100 X 100의 2차원 배열을 만들면 메모리 용량 초과로 문제를 맞게 풀려도 틀리게 채점이 될 것이다. 따라서 이런 유형의 문제에서는 토글링을 쓰거나 작은 배열을 만들어서 풀면 된다.
이 문제에서는 1차원 배열 dp를 만들어서 풀면 된다.
dp [i] = j, 여기서 i = 금액, j = i원을 만들 수 있는 경우의 수로 정의하겠다.
이 문제의 점화식은 다음과 같다.
→ dp [i] = dp [i] + dp [i - coin] 단, i - coin == 0이면 dp [i] = dp [i] + 1
예제를 예로 한번 보겠다.
동전의 개수 n = 3이고 k = 10원이다. 따라서 1원, 2원, 그리고 5원짜리 동전으로 10원을 만들 수 있는 경우의 수를 구해야 한다.
1. 1원짜리 동전으로 1원부터 10원까지 만들 수 있는 경우의 수를 구한다.
2. 2원짜리 동전으로 10원까지 만들 수 있는 경우의 수를 구한다. 단, 여기서 1원으로 구한 값을 이용해야 한다. 만약에 1원으로 구한 값을 이용을 안 하면 계산해야 되는 개수가 너무 많아지고 이것은 DP가 아니다.
3. 5원짜리 동전으로 10원까지 만들 수 있는 경우의 수를 구한다. (2원으로 구한 값을 재이용한다.)
1원짜리 동전 이용 시 dp 값
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10(원) |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
2원짜리 동전 이용 시 dp 값
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10(원) |
| 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 | 5 | 6 |
5원짜리 동전 이용 시 dp 값
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10(원) |
| 1 | 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 10 |
따라서 예제의 답은 10이 된다.
- 코드
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
int[] dp = new int[k+1];
for (int t = 0; t < n; t++) {
int coin = Integer.parseInt(br.readLine());
for (int i = 1; i <= k; i++) {
if (i - coin > 0) {
dp[i] = dp[i] + dp[i-coin];
} else if (i - coin == 0) {
dp[i]++;
}
}
}
System.out.print(dp[k]);
}
}
- 후기
코드를 보면 그렇게 길지 않고 1차원 배열을 이용한 DP 문제인 것을 확인할 수 있다. 그런데도 불구하고 이 문제를 풀기까지 되게 많은 시간이 걸렸다. 그리고 어떻게 풀어야 하는지 생각이 안 나서 많이 헤매기도 했다. 이런 걸 보면 아직은 너무나도 부족한 거 같다.
'백준' 카테고리의 다른 글
| [백준] 1697번 : 숨바꼭질 – JAVA [자바] (0) | 2022.02.11 |
|---|---|
| [백준] 9465번 : 스티커 – JAVA [자바] (0) | 2022.02.11 |
| [백준] 2583번 : 영역 구하기 – JAVA [자바] (0) | 2022.02.04 |
| [백준] 10026번 : 적록색약 – JAVA [자바] (1) | 2022.01.31 |
| [백준] 15482번 : 한글 LCS – JAVA [자바] (0) | 2022.01.30 |




댓글