목차
Security Principles: CIA Triad
Confidentiality (기밀성) :
Integrity (무결성):
Availability (가용성):
Normal Communication

Eavesdropping (도청)

Eavesdropping: 도청 (보내는 메시지 read)
Tampering (부당 변경)

Tampering: 부당 변경 (보내는 메시지 modify 해서 보냄. 수신자는 변경된 메시지 받음)
Blocking

Blocking: 보내는 메시지 remove.
Cryptography (암호 작성술)
Cryptography ensures the confidentiality (비밀성) and integrity (무결성) of the message (not availability).
Confidentiality: Cryptography ensures confidentiality by encrypting the data, making it unreadable to anyone who doesn't possess the decryption key. This prevents unauthorized access to sensitive information.
Integrity: Cryptography ensures integrity by using techniques such as digital signatures or message authentication codes (MACs). These methods verify that the data has not been altered in transit or storage. Even minor modifications to the data would result in a significant change in the cryptographic signature, alerting the recipient to potential tampering.
Availability:
- Key management: Cryptography relies on keys for encryption and decryption. If these keys are lost or inaccessible, the data becomes unavailable.
- DoS attacks: Cryptography cannot prevent DoS attacks, where an attacker floods a system with traffic or requests, overwhelming its capacity and making it inaccessbile to legitimate users.
- Hardware or software failures: Cryptography relies on underlying software and hardware. Failure can lead to unavailibility of data, even if it remains confidential and intact.
Kerckhoff's principle
The security provided by an encryption system should not depend on the secrecy of the system, but only on the secrecy of the key.
케르크호프스의 원리: 암호체계의 안전성은 키의 비밀성에만 의존해야한다.
Encrypted Communication

Encryption and decryption are computationally infeasible without the encryption and decryption keys.
Symmetric Encryption

Encryption and decryption keys are the same.
Decryption is the reverse of encryption.
How to share the key?
Symmetric Key Distribution

Each pair needs a distinct key.
A quadratic number of keys for pairwise communication.
Classic Protocols
Julius Caesar's Cipher
Encryption: Shift letters by 3.
- A --> D
- B --> E
Encryption: Forward alphabet shift + 3
Decryption: Reverse alphabet shift - 3
Example
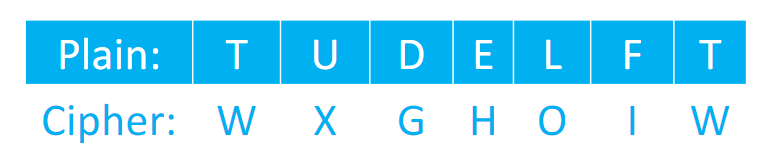
Alphabet Shfit Cipher
Generalized Caesar's cipher
Key = k
Encryption: Replace each character with the character k positions after it in the alphabet
Decryption: Replace each character with the character k positions before it in the alphabet.
Not used today --> insecure
Guess key k: Try all possible values of k, find the one where the decryption makes sense.
Question

답: B
반대로 -2 하면 됨
Substitution Cipher
Permutation of the alphabet characters:
e.g. A --> L, B --> Z
Key = Permutation
Number of possible keys for a 26-character alphabet ≒ 4 x 10^26
Impossible to try all possible keys
Can be cracked by frequency analysis (빈도 분석)
English language:
- Most frequent letters: e, t, o, a, n, i
- Most frequent diagrams: th, in, er
- Most frequent trigrams: the, and, ...
많이 쓰는 언어를 토대로 유추
Example:

여기서 LBO가 자주 등장하는데 이거를 가장 많이 쓰는 and, the 등으로 가정. 혹은 아래에 있는 사진처럼 Plaintext에 있는 알파벳의 빈도와 평상시에 많이 사용되는 빈도를 비교해서 유추.

여기서 L = T, B = H, O = E로 유추를 해보겠다. 그리고 Plaintext를 변환하면 다음과 같이 된다.

그다음에는 J = R, K = S, X = A로 유추를 해보면 Plaintext는 다음과 같이 된다.

이 방식을 반복하다 보면 다음과 같은 해독된 메시지, 즉 decrypted message를 구할 수 있다.

One-Time Pad (1회용 암호표)
Highest level of security
Built based on the Bitwise XOR

Key:
- Sequence of random bits
- Same length as plaintext (really long key - one of the disadvantage)
Encryption
C = K ⊕ P
- P = 01101001
- K = 10110010
- C = 11011011
Decryption
P = K ⊕ C (반대로 XOR 하면 Key와 Ciphertext를 이용해서 Plaintext 구할 수 있음)
Advantages
- Each bit of the ciphertext is random
- Fully secure if key used only once (one-time pad has perfect secrecy assuming a truly random and secret key that has not been reused)
All messages are equally possible given a ciphertext
Disadvantages
- Key as large as plaintext (Difficult to generate and share)
- Key cannot be reused (if key reused, possible to infer the key)
One-Time Pad has perfect secrecy no matter the adversary (상대방), the schema cannot be broken.
- Assuming a truly random and secret key that has not been reused.
Question

답: A
→ Key와 Message XOR 하기.
One-Time Pad Pitfalls: Key Reuse

XOR two ciphertexts (can see both the text and the smiley face)
One-Time Pad Pitfalls: Imperfect Randomness

If there is a bit of randomness, some information can be leaked (encrpyted but can kind of tell)
→ For one time pad, need random keys
Modern Symmetric Encryption Standards
Data Encryption Standard (DES)
- Key is only 56-bits long
- Attack: Exhaustive search over the key space (56 비트 밖에 안 되서 현재는 사용 X)
Advanced Encryption Standard (AES)
- Key can be 128, 192 or 256 bits
- Exhaustive search not possible
→ Use AES (not DES) for symmetric encryption
Cryptographic Hash Functions
Hash Functions

Collsion: two different inputs get the same output (same hash value)
Hash Functions - Collisions
A collision occurs when two messages have the same hash value
Inevitable if there are more inputs than outputs
If two hashes are different, the inputs are different
Two inputs could have the same hash
Cryptographic Hash Functions
Short output
The hash value has a small and fixed length (e.g. 256 bits)
One-way
Given a hash value, it's really hard to find a message with it (되돌아갈수 없음)
→ Given a hash value x, it is hard to find a plaintext P such that h(P) = x
Collision resistance
Given a message, it's hard to find a different message with the same hash value
Weak collision resistance: Given a plaintext P, it is hard to find a plaintext Q such that h(Q) = h(P)
Strong collision resistance: It is hard to find a pair of plaintexts P and Q such that h(Q) = h(P)
Public function: No secret key, everyone can compute it
Only feasible attack is brute-force, try all possible messages
Applications
Problem File Integrity:
- A stores his files in a cloud server managed by B
- A later receives the files
- What if B tampered with the files?
Solution
Compute the cryptographic hash of each file and stores them locally
Check the cryptographic hashes of the retrieved files againt the stored ones
Weak collision resistance (given a plaintext P, hard to find a plaintext Q with same hash output) makes it difficult to change the file to one with the same hash value.
Problem: Password Authenticate
How to authenticate users without storing passwords?
We want to avoid server breach that leaks passwords
We want to defend against password-guessing attacks
Solution:
Store crypto hash of password but not the password
One-way makes it difficult to recover password from hash
Weak collision resistance makes it hard to guess other password with same hash
Problem: Coin tossing online
Want to generate a random bit {0, 1}
Is there a fair protocol?
Solution:
Agree on a crypto hash function h
Pick a random integer R and send d = h(R)
Guess whether R is odd or even
Reveal R
If guess was correct, output 1 else 0
Need all three properties:
- One-way property ensures that Harm cannot derive R from h(R).
- Weak collision resistance ensures that Harm cannot guess some value S, such that h(S)=h(R)
- Strong collision resistance ensures that George cannot find an odd value S and an even value R, such that h(S)=h(R), and then reveal the value that sets the coin toss in his favor.
Birthday Attack
Probability that two people in a group share a birthday
= Probability of repetitions in a sequence of random values (0 to n - 1)
- About 50% probability for a sequence of length √n
Brute-force attack on strong collision resistance:
- Find a pair of planitexts P and Q such that h(Q) = h(P)
- Let b be the number of bits of the hash function
- Continuosly generate plaintexts and hashes
- Number of tries until we succeed (find a colliding pair) with 50% probability = 2 ^ (b / 2) tries
With 50% probability: H(Pi) = H(Pj)
Question

답: A, B
A: One way (cannot recover)
B: Need also weak collision resistance (cannot find another password that has the same hash value, so gets authenticated)
Entropy
엔트로피: 시스템 내 정보의 불확실성 정도를 나타내는 용어
Entropy: Formal measure of uncertainty in the outcome of a process
Information

Higher probability → Less information
Measured in bits
Example:

Question

답: C (2 bits)

Entropy
Average value of information we obtain by learning the result of Experiment E, with outcomes e0, e1, ..., en-1
General Rule:
- Event with n possible outcomes
- Each outcome is equally likely
Entropy = log (n) bits

Example:
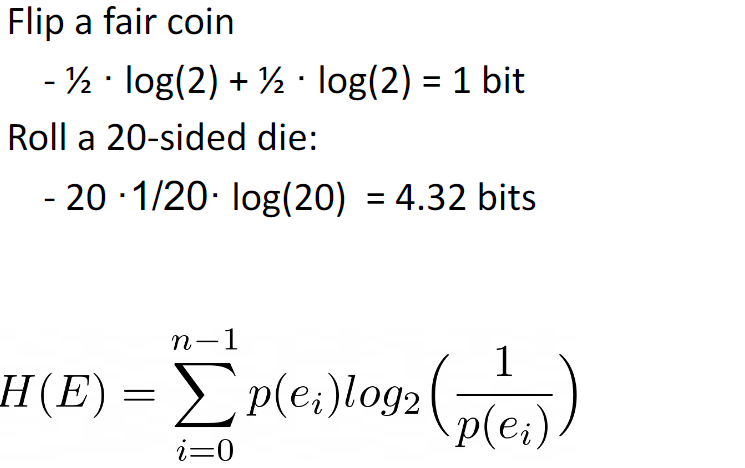
Question

답: C = 1.5 bits

'학교 > CS' 카테고리의 다른 글
| Lecture 10: Cryptography 3 (1) | 2024.04.07 |
|---|---|
| Lecture 9: Cryptography 2 (1) | 2024.04.07 |
| Lecture 7 pt 2: Background for Software Security and Testing (0) | 2024.03.18 |
| Lecture 7 pt1 : Database Security (0) | 2024.03.18 |
| Lecture 6: OS - Level Security (0) | 2024.03.03 |




댓글