목차
Block Cipher
A block cipher is a symmetric encryption scheme for messages (blocks) of a given fixed length
- The length of the block is independent from the length of the key
AES is a block cipher that operates on blocks of 128 bits (16 bytes0
- AES supports keys of length 128, 192, and 256 bits
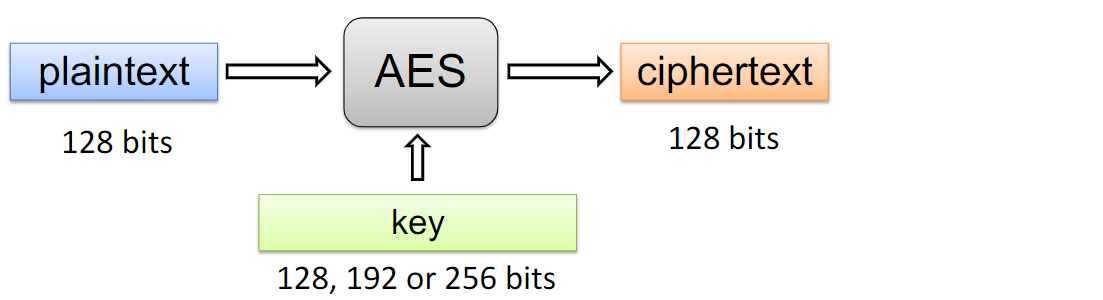
ECB Mode
When plaintext is longer than block size, b
- Partition plaintext P into sequence of m blocks P[0], ... , P[m - 1], where n/b <= m < b/n + 1
Electronic Code Book (ECB) Mode
- Assume n is multiple of b
- Block P[i] encrypted into ciphertext book C[i] = E
Properties:
- Documents and images are not suitable for ECB (Documents and images have patterns that can be exploited)
- ECB works well with random string
- Encryption can be done in parallel
Question

답: B

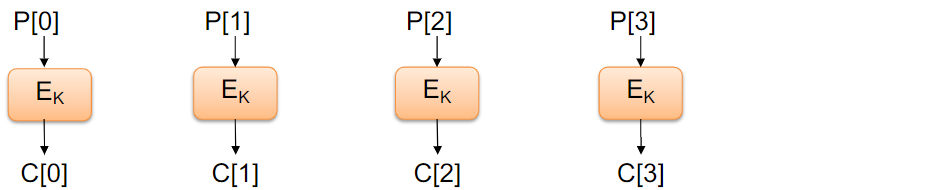
CBC Mode
Cipher Block Chaining (CBC) Mode
- Previous ciphertext block combined with current plaintext block C[i] = E_k(C[i - 1] ⊕ P[i])
- C [-1] = V is a random block (initialization vector) sent encrypted during setup
Each ciphertext depends on the previous one

Properties:
- Works well with any input plaintext (documents, images, ...)
- Requires the reliable transmission of all blocks
→ Not suitable for applications that allow packet losses E.g. audio and video streaming
- Can't parallelize like ECB Mode
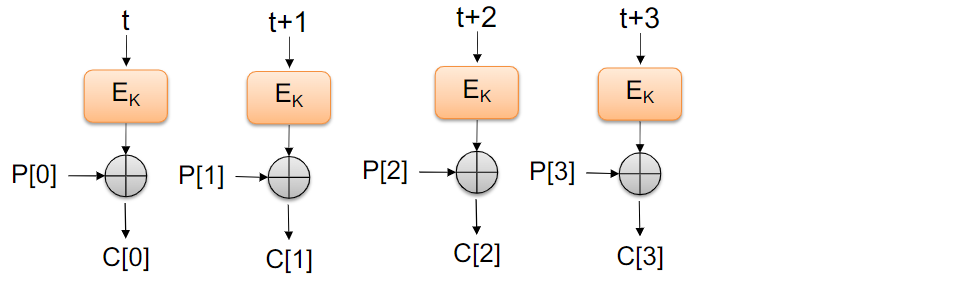
Counter Mode
To not reveal patterns and work in parallel:
→ Counter Mode:
- Counter t
Encryption: C[i] = E_k (t + i) ⊕ P [i]
No need to implement decryption (저 공식에서 쓸 수 있는듯)
Padding
Block ciphers require the length n of the plaintext to be a multiple of the block size b
How to pad unambiguously the last block?
Pad is a sequence of identical bytes, each indicating the length (in bytes) of the padding
Example for b = 128 (16 bytes)
- Plaintext: "Bernardo" (7 bytes)
- Padded plaintext: "Bernardo999999999" (16 bytes)
We need to always pad the last block, which may consist only of padding
Question

답: D

Stream Cipher
One-Time Pad
Key: Sequence of random bits, same length as plaintext
Encryption: C = K ⊕ P
Decryption: P = K ⊕ C
Advantages
- Each bit of the ciphertext is random
- Fully secure if key used only once
All messages are equally possible given a ciphertext
Disadvantages
- Key as large as plaintext (difficult to generate)
- Key cannot be reused
Stream Cipher
Key Stream:
- Pseudo-random bit sequence generated from a secret key K

- Generated on-demand, one bit (or block) at the time
Stream cipher: XOR the plaintext with the key stream C[i] = Sk[i] ⊕ P[i]
This is symmetric key encryption

Advantages:
- Fixed-length secret key
- Plaintext can have arbitrary length (e.g. media stream)
- Incremental encryption and decryption
- Works for packets sent over an unreliable channel
Disadvantages:
- Key stream cannot be reused
Key Stream Generation
Block cipher in counter mode
- Use a block cipher Ek with block size b e.g. AES (block size is 128)
- The secret key is a pair (K, t), where K is a key and t is a counter with b bits
- The key stream is the concatenation of ciphertexts: Ek (t), Ek (t + 1), Ek (t + 2)
Advantages
- Simplicity
- Speed
Disadvantages
- Very long key streams can be distinguished from random
Initialization Vector
Goal: Avoid sharing a new secret key for each stream encryption
Solution:
- Use a two-part key (U, V)
- Part U is fixed
- Part V is transmitted together with the ciphertext
- V is called initialization vector
Setup: Alex and Harm share secret U
Encryption:
- Alex picks V and creates key K = (U, V)
- Alex creates stream ciphertext C and sends (V, C)
Decryption:
- Harm reconstructs key K = (U, V)
- Harm decrypts the message
Attacks on Stream Ciphers
Repetition attack
- Stream reuse yields XOR of plaintexts
- Cryptanalysis can recover the original plaintexts
Replacement attack
- P = A B C, where the attacker knows B
- Enc (P) = K L M
- By computing B ⊕ L, part of the key stream is revealed.
- The attacker can derive the ciphertext of Q = A D C
Question

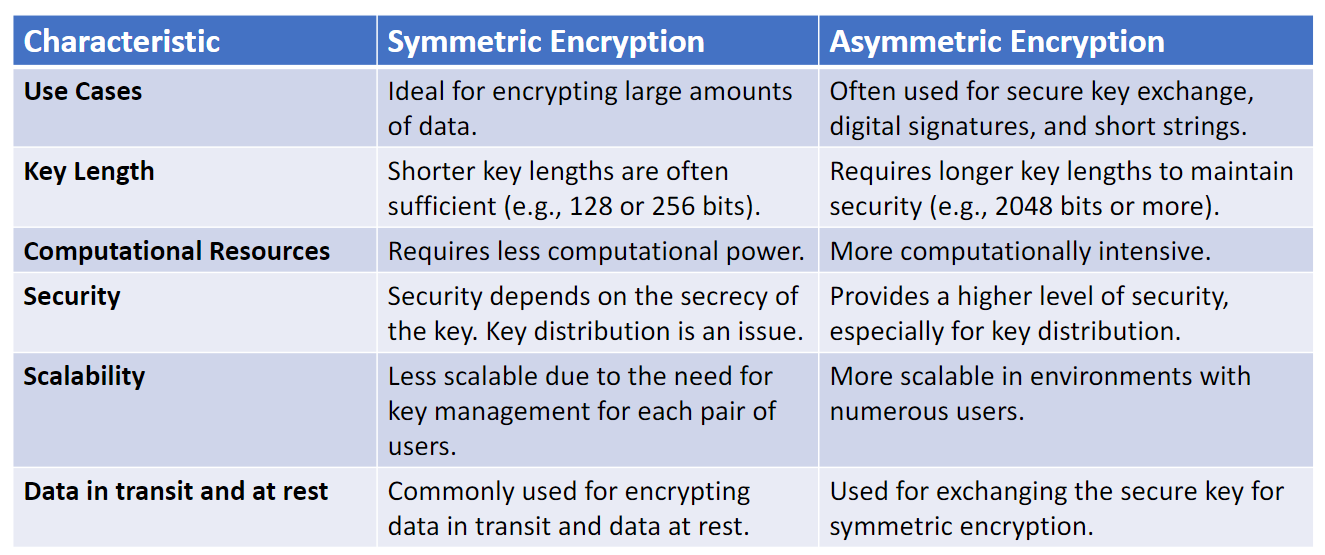
Public Key Cryptography
Key pair:
- Public key: shared with everyone
- Secret key: kept secret, hard to derive from the public key
Protocol:
- Sender encrypts using recipient's public key
- Recipient decrypts using his secret key


Public-Key Encryption in Formulas
Notation:
- PK: Public key of recipient
- SK: Secret key of recipient
- (PK, SK) = KeyGen()
- M: plaintext
- C: ciphertext
Encryption:
- C = Enc_PK (M)
- The sender encrypts the plaintext M with the public key of the recipient
Decryption:
- M = Dec_SK (C)
- The recipient decrypts the ciphertext with their private key
Properties:
- Anyone can encrypt a message since the recipient openly shares the public key
- Only the recipient can decrypt the message since the private key is kept secret
- It should be infeasible to derive the secret key from the public key
Advantages:
- A single public-secret key pair allows receiving confidential messages from multiple parties
Disadvantages:
- Conceptually complex
- Slower performance than symmetric cryptography
RSA
Most widely used public key cryptosystem today
Depends on factoring being hard
2048-bit (or longer) keys recommended (126 bits in AES)
Much slower than AES (have to deal with exponentiation)
Typically used to encrypt an AES symmetric key
Threat Models
(Weaker) Adversary Models
Ciphertext-only:
- Adversary sees all ciphertexts, but has no / vague information about the underlying plaintext
Known plaintext:
- Adversary also knows part of / format of plaintext messages
How could this happen?
- All of your internet requests start with the same header
- Sending a CSV in the same format every week
- You text "hi" to people when you first start texting them
Open design principle
(Stronger) Adversary Models
Chosen plaintext
- Adversary is able to encrypt plaintexts of their choosing and see the resulting ciphertexts
How can this happen?
- Harm sends Alex an email saying "Please securely forward this to George"
- Public key cryptography
Chosen ciphertext
- Adversary chooses ciphertexts and some info is revealed about the decryption
Formalization
How do we show that our schemes are secure against these different kinds of attacker models?
Goal: Cryptosystem should not leak any information about the plaintext M.
Idea: No adversary should be able to distinguish between two messages based on their encryption
We model security of encryption schemes as a game:
- Played between a challenger (with access to the encryption algorithm and the secret key) and an adversary
IND-CPA
Indistinguishability under Chosen Plaintext Attack
Adversary has polynomially-bounded access to an encryption oracle
→ Computationally-bounded
Adversary has polynomially-many (m, c) pairs for m's of their choosing

Query phase: Sends the message m and gets the ciphertext c
Challenge phase: Picks two messages,
If adversary's probability of winning the game is approximately ½, then our scheme is "IND-CPA secure"
Question
Is the Caesar cipher cryptosystem IND-CPA secure?
답: No
Query phase: Not necessary
Challenge phase: Send plaintexts "AB" and "AA"
- If output is in the form "XY" (where X =! Y), then output "AB"
- Otherwise, output must be in form "XX"; then output "AA"
Question
Is the one-time pad cryptosystem IND-CPA secure?
답: No
Query phase: Send messages m1, m2 to get c1, c2
Challenge phase: send plaintexts m1, m2; challenger returns c_i
- if c_i ⊕ c1 = 0, then output m1
- otherwise, it must be that ci ⊕ c2 = 0, so output m2
Question
Can a determnistic encryption scheme be IND-CPA secure?
답: No
Query phase: send message m1 to get c1
Challenge phase: send message m1 and some other m2; challenger returns c_i
- if ci = c1, then output m1
- otherwise, output m2
Question
Is the encryption function Enc_k (m) = 1 IND-CPA secure?
Yes, but it's not correct. We also care about correctness - i.e. that we can actually decrypt a given encryption
IND-CCA
Indistinguishability under Adaptive Chosen Ciphertext Attack
Adversary has polynomially-bounded access to an encryption oracle and a decryption oracle
Even after the challenge
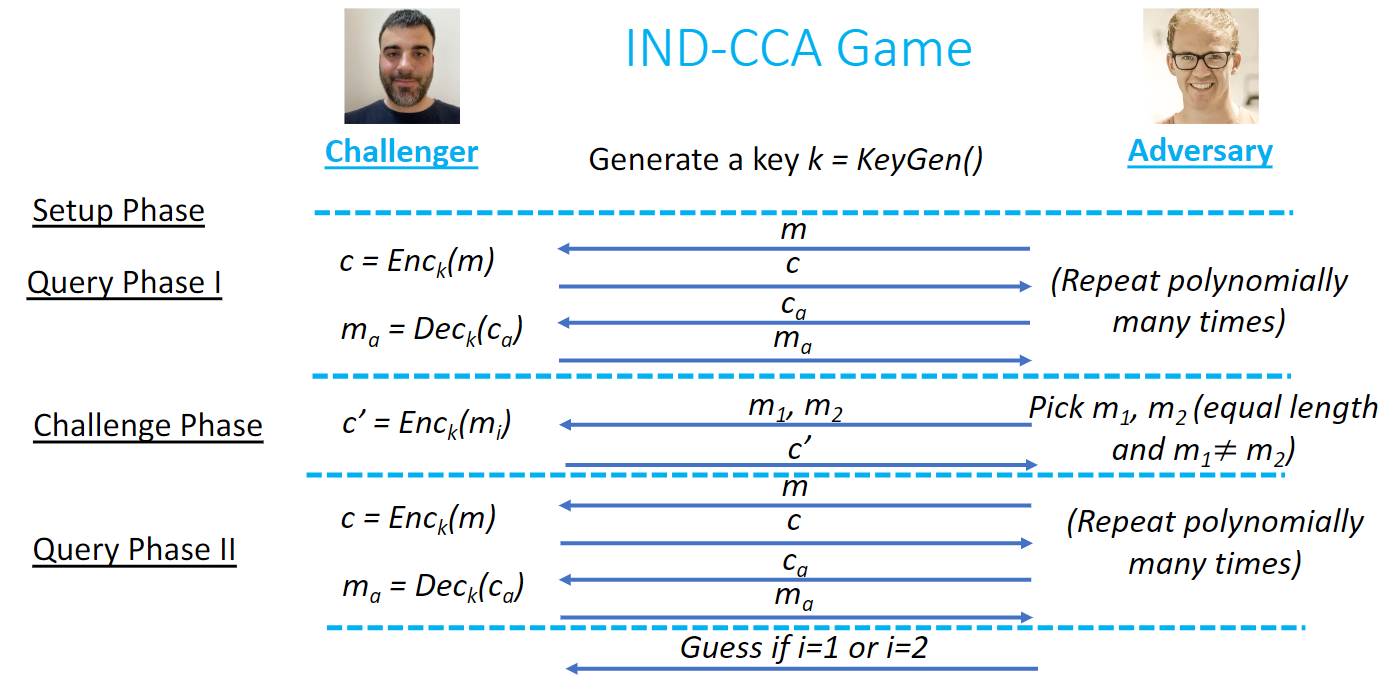
Question

답: No
Pick m0 = 00...00 and m1 = 11...11
c' = Enc(m_i)
Create a ciphertext consisting of the first half of c' and some other ciphertext for the second half
Send it to the decryption oracle
This returns the first half of m_i → Adversary wins
'학교 > CS' 카테고리의 다른 글
| Lecture 11: Cryptography 4 (0) | 2024.04.08 |
|---|---|
| Lecture 10: Cryptography 3 (1) | 2024.04.07 |
| Lecture 8: Cryptography 1 (1) | 2024.04.06 |
| Lecture 7 pt 2: Background for Software Security and Testing (0) | 2024.03.18 |
| Lecture 7 pt1 : Database Security (0) | 2024.03.18 |




댓글