목차
Password Authentication

→ Attacker can attack on the client side, network and the server.
How should the server store passwords?
Our goal is to defend from attacks that exfiltrate the password database stored by the server (DB에 있는 비밀번호를 얻으려고 하는 행위로 부터 방어)
- Most common password-related attack on server
We don't consider other password attacks on the server
- Eavesdropping passwords submitted by users
- Modigying the password authentication code
Store the passwords in plaintext
If database is stolen, so are the passwords
Admin have direct access to users' passwords

Store the passwords encrypted
Store passwords encrypted with keys
If encrypted passwords are stolen, what prevents the key from being stolen?
Anyone with the key (admin) can view password

Hashing the Passwords
Identical passwords produce identical hashes (problem when a lot of users use the same password -> crack one hash, can crack everybody else)
Once you've cracked a given hash, you can trivially crack it every tiem you see the same hash again
Humans pick bad passwords (common passwords → frequent analysis 통해 비밀번호 알아낼 수도 있음)

Hashing the Passwords with One Salt
Generate a salt (random string)
Hash all passwords with the salt
→ Hash the given password with the salt and compare

Disadvantages
- Identical passwords and identical salts produce identical hashes
- Humans pick bad passwords → frequency analysis
- If you crack one password, you crack all identical ones
- For big sites, precomputation is worth it
Hashing Passwords with Per-User Salting
Generate a salt (random string) for each user
Hash the passwrd with their salt, store salt and ahsh
- Hash the given password with the user's salt and compare

Advantages
- Since every user has different salt, identical passwords will not have identical hashes
- No frequency analysis
- No using known passwords to crack other passwords
- No precomputation, hence much harder to crack
Question

답: B (Yes, a fraction of them)
설명:
Identical passwords produce identical ciphertexts
If you know one password, you know all passwords with the same ciphertext
Humans pick bad passwords and hints: Frequency Analysis, Password hints, Unique passwords with good hints are safe
Password Complexity: Size of Password Space
6-character password with only lower case letters, no numbers or symbols
There are 26 × 26 × ... × 26 = 26^6 possible passwords
Easy to try all of them (password can be found by brute forcing)
→ Increase the password length (also allow for more characters)
Password Cracking
Brute Force
Try all passwords in a given space → this process is parallelizable
Eventually succeeds given enough time and computing power
Large computational effort for each password cracked
Dictionary Attack
Precompute hashes of a set of likely passwords → Parallelizable
Store (hash, password) pairs sorted by hash
Fast look up for password given the hash
Requires large storage and preprocessing time
A dictionary attack uses a preselected library of words and phrases to guess possible passwords. It operates under the assumption that users tend to pull from a basic list of passwords
→ 자주 사용하는 비밀번호들의 hash 미리 계산해서 저장해놓고 시도하는 방법.
Intelligent Guessing Methods
Try the top N most common passwords
Dictionary of words, names, places, notable dates and try combinations of the these
Can also train Markov Chain Model with common passwords
For any scheme that involves guessing, the time to crack is reduced by guessing intelligently
Key insight: Not all passwords are equally likely
Idea: Try most likely passwords first
Question

답: A, B or C
설명: Depends on the assumptions you make:
→ Policy B has bigger password space, though users can pick bad passwords (i.e. password, 12345678)
→ If both policies prevented users from picking common passwords, then B
Secret Sharing
How to share key s?
1-out-of n Secret Sharing
Everyone knows s

Drawbacks:
- What if one of them gets kidnapped?
- What if not everyone is trusted?
n-out-of n Secret Sharing
Split s into 3 shares
Everyone is needed to reconstruct s from the shares

Trusted Dealer:
1. Pick s0 and s1 randomly
2. s2 = s ⊕ s0 ⊕ s1
Secret Recovery:
s = s0 ⊕ s1 ⊕ s2
= s0 ⊕ s1 ⊕ s ⊕ s0 ⊕ s1 (위 공식: trusted dealer)
= (s0 ⊕ s0) ⊕ s ⊕ (s1 ⊕ s1)
= (00...00) ⊕ s ⊕ (00...00)
= s
Information Theoretic Security:
- No information about s can be recovered from fewer than all shares
With fewer than 3 shares, all possible secrets are equally likely
For any s_fake and shares s0, s1:
s2 = s_fake ⊕ s0 ⊕ s1
Drawbacks:
- What if someone loses their share (s 만드려면 다 필요함)
- What if no consensus is reached?
Can only two shares suffice to recover s? → 2-out-of-n secret sharing
2-Out-Of-n Secret Sharing
Any two shares are sufficient to recover s
Lines
Let's say the secret is s = 42
Consider f(x) = 10x + 42, where 10 was picked randomly.
The secret is recovered by computing f(0)
Each user is given a share, which is a point of f. Any two users can recover f.
→ 두 개의 점을 이용해서 line equation 구한다음 intercept 구하면 그게 s
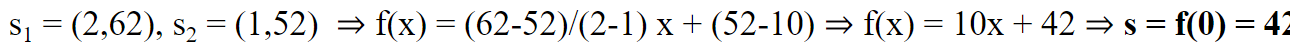
t-out-Of-n Secret Sharing
Any t shares are sufficient to recover s
Polynomials: t district points define exactly one polynomial of degree t - 1
Information Theoretic Security:
- No information about s can be recovered from fewer than t shares
- With fewer than t shares all possible secrets are equally likely

Secret Sharing
A t-out-of-n secret sharing scheme:
Share(s) returns s1, s2, ..., sn
Recover(sk, ..., s_k+t-1) returns s
Correctness
For any subset S_t of Share(s) of sizt t: Recover(S_t) = s
Security:
Using any subset of Share(s) of size smaller than t, absolutely nothing can be learned about s.
Shamir Secret Sharing (샤미르의 비밀 공유)
A Trusted Dealer must compute Share(s).


Lagrange interpolation to determine the polynomial and substitute value 0 to recover the secret
Advanatages
- Information Theoretic Security (impossible to break even with infinite computational power)
- Small shares (just poitns)
- Security can be adjusted by updating the polynomial (and re-issuing shares)
- A different number of shares can be issued to each user
Drawbacks
- Participants can cheat (Shares could be incorrect, nobody knows if the secret is correct or not)
- Total trust in the dealer
Question

Applications
End-to-End encryption e.g. Messaging
Cryptocurrency e.g. Bitcoin
DNS
Anonymization Networks
Privacy with HTTPS
Alice connects to Bob through her ISP (Internet Service Provider)

VPN
Route communication from source to destination via intermediate relay node
- Communication from source to VPN relay typically encrypted and authenticated
- Overhead due to additional link
VPN usage shifts visibility of communication endpoints from ISP to VPN provider

Onion Routing
Extend the notion of VPN by using sequence of intermediate relays
- Under different administrative domains
- Possibly located in different jurisdictions (관할권)
→ Elude who is sending the mssage
Cost-benefit tradeoff:
- Additional relays increase anonymity but slow down communication

Onion Model
Network of relays (aka nodes or routers) - known public keys of relays
Message sent via random sequence of relays (circuit)
- First relay: entry node or guard node
- Intermediate relays
- last relay: exit node

Provide privacy → can communicate anonymously
Onion Encryption and Routing
Layered encryption
- Header: next node
- Payload: message for next node, encrypted for relays
Routing:
- Decrypt and forward to next node (R1 receives the payload/message and decrypts it and figure out that R2 is the next node...)
Each node knows previous and next

R1이 받을 때는 E_k1 상태로 되어 있음. 이걸 해독해야 다음에 어떤 node에 보낼지 알게됨.
Onion Routing Properties
Privacy goal: support anonymous communication
- Prevent linking of sender to receiver (중간에 relay nodes들이 이 역할)
Specific privacy properties:
- Recipient does not know who is sender (unless sender reveals it in message)
- Administrator of relay cannot link sender to recipient (unless it controls all relays of circuit)
- Network eavesdropper cannot link sender to recipient (unless it observes traffic at all relays of circuit)
Onion Routing in Practice
Do not encrypt final hop - encryption may be done by application (e.g. https)
Source sets up:
- Random circuit (route)
- Symmetric keys shared with routers
Data tunneled to final router over circuit
Exit node issues DNS query

Internet Censorship
Control or suppresion of the publishing or accessing of information on the Internet
Carried out by governments or by private organizations
Individuals and organizations may engage in self-censorship on their own or due to intimidation and fear
Censoring Techniques
DNS Blacklist:
- DNS does not resolve domain names or returns incorrect IP address
e.g. www.google.com → 'page not found'
IP Blacklist:
- For sites on a blacklist, the censoring system prevents connection attempts
Keyword Blacklist:
- The censoring system scans the URL string and interrupts the connection if it contains keywords from the blacklist
TOR : The Onion Router
Access normal internet sites anonymously, and Tor hidden services
TOR helps to defend against a form of network surveillance that threatens personal freedom and privacy
Question

TOR Analysis
Advantages:
- Creates a tunnel, allows it to work with any protocol
- Three nodes of proxying, each node not knowing the one before last, makes very difficult to find the source
Problems:
- Slow (high latency)
- Exit node? (may have to connect to not wholesome website)
- Semi-fixed infrastructure: possible to block all Tor relays listed in the Directory
- Fairly easy totell someone is using it from the server side (easy to track)
- Might raise suspicions of illegal activity
How to Block Tor?
Attackers can block users from connecting to the Tor network
- Blocking the directory authorities (directory authorities are special relays that keep track of which relays are currently running)
- Blocking all the relay IP addresses in the directory
- Preventing users from finding the Tor software
Bridge relays
Rather than signing up as a normal relay, you can sign up a special bridge realy that is not listed in any directory
No need to be an exit (so no abuse worries), and you can rate limit if needed
'학교 > CS' 카테고리의 다른 글
| Lecture 13: Malware and Malware Detection (0) | 2024.04.08 |
|---|---|
| Lecture 12: Software Security and Testing (1) | 2024.04.08 |
| Lecture 10: Cryptography 3 (1) | 2024.04.07 |
| Lecture 9: Cryptography 2 (1) | 2024.04.07 |
| Lecture 8: Cryptography 1 (1) | 2024.04.06 |




댓글